Online-Bibliothek

Differentialrechnung

[905] Differentialrechnung (Ableitungsrechnung, Derivationsrechnung, Derivationskalkül) und Integralrechnung (s.d.) bilden zusammen den Grundstock der ganzen höhern Mathematik, und auf ihnen beruht in erster Linie die Überlegenheit der neuern Mathematik über der der Alten. Mit ihrer Hilfe können zahllose Aufgaben der Geometrie, Mechanik, Astronomie und Physik, die sonst kaum angreifbar oder überhaupt unzugänglich sind, durch Gleichungen ausgedrückt und damit auf rein mathematische Aufgaben zurückgeführt werden, die sich dann entweder ganz genau oder doch mit jedem beliebigen Grade von Genauigkeit durch Rechnung lösen lassen. Von grundlegender Bedeutung ist hierbei der Begriff der Funktion. Eine veränderliche Größe v heißt eine Funktion der Veränderlichen x, y, z etc., wenn zu beliebig gewählten Werten von x, y, z etc. stets ein Wert (oder mehrere Werte) von v gehört, der nach irgend einem Gesetze durch die Werte von x, y, z etc. bestimmt ist oder aus ihnen berechnet werden kann. Man schreibt dann v = f (x, y, z,), gelesen v gleich f von x, y, z etc. und nennt x, y, z... die unabhängigen Veränderlichen oder auch die Argumente der Funktion, v die abhängige Veränderliche. So ist z. B. die Temperatur auf der Erdoberfläche eine Funktion von vier Veränderlichen: der Zeit, der geographischen Länge, der geographischen Breite und der Höhe des Beobachtungsorts über dem Meeresspiegel. Für f setzt man oft auch andre Buchstaben, φ, ψ etc., als Funktionszeichen. Die D. untersucht zunächst Funktionen einer unabhängigen Veränderlichen x; die abhängige Veränderliche wird dann meist y genannt. Beispiele solcher Funktionen sind: y = x², y = ¹, x, y = √x, y = sin x etc., das allgemeine Zeichen einer Funktion ist: y = f (x) oder y = φ(x) etc. Gehört zu jedem Werte von x nur ein Wert der Funktion, so heißt die Funktion eindeutig oder einwertig, wie z. B. die Funktionen y = x², y = ¹/x, y = sin x. Gehören zu jedem Werte von x zwei oder mehrere Werte von x, wie z. B. bei der Funktion y = √x, der man entweder das+oder das-Zeichen geben kann, so heißt die Funktion mehrdeutig oder mehrwertig. Eine mehrdeutige Funktion muß man zuerst eindeutig machen, indem man z. B. bei y = √x nur die positiven oder nur die negativen Werte der Wurzel ins Auge faßt. Liefert der Wert x des Arguments den Wert y = f(x) der Funktion, so liefert der Wert x+Δx des Arguments den Wert y+Δy = f(x+Δx) = f(x)+Δf(x), und man nennt Δy (gelesen Delta-y) oder Δf = f (x+Δx)-f(x) den Zuwachs, den die Funktion erhält, wenn das Argument um, Δx wächst. Läßt man Δx immer kleiner werden und der Null immer näher kommen und kommt dabei. Δf ebenfalls ohne Aufhören der Null immer näher, so sagt man: die Funktion f (x) ist für den betreffenden Wert des Arguments x stetig oder kontinuierlich, im entgegengesetzten Fall ist sie unstetig oder diskontinuierlich. So ist die Funktion y = x² für jedes endliche x stetig, weil Δy = (x+Δx)²-x² = (2 x+Δx).Δx; die Funktion y = ¹/x aber ist nur stetig, solange x nicht verschwindet, für x = 0 dagegen unstetig, denn für sie ist: Δy = 1/(x+Δx)-1/x = -Δx/x(x+Δx)²

was für x = 0 unendlich groß wird, wie klein man auch Δdx wählen mag. Der Bruch:[905]

(1)

dessen Zähler die Differenz der Funktionswerte f(x+Δx) und f(x) und dessen Nenner die Differenz der zugehörigen Argumente x+Δx und x ist, heißt der Differenzenquotient der Funktion. Für y=x² und y = ¹/_x findet man der Reihe nach:

In beiden Fällen läßt sich Δy/Δx, als eine Summe zweier Teile darstellen, von denen der erste (2x und -1/x²) von Δx frei ist, während der zweite immer kleiner wird, je kleiner man Δx wählt, und für Δx=0 verschwindet. Man nennt nun die Funktion f(x) differentiierbar, wenn sich der Differenzenquotient (1) so wie in diesen Beispielen in der Form:

(2)

darstellen läßt, wo f'(x) eine neue Funktion von x allein ist, während φ von x und Δx abhängt, aber der Null immer näher kommt, je mehr Δx sich dem Werte Null nähert und schließlich für, Δx = 0 verschwindet. Die Funktion f'(x) (gelesen f gestrichen x) heißt die abgeleitete (derivierte) Funktion oder die Ableitung von f(x). Setzt man in (1) Δx = 0, so wird auch f(x+Δx)-f(x) = 0 und der Differenzenquotient verliert seine Bedeutung. Aber (2) zeigt, daß sich Δf/Δx, je näher Δx der Null kommt, um so mehr dem Werte f'(x) nähert, daß also die Ableitung f'(x) der Grenzwert (Limes) ist, dem der Differenzenquotient zustrebt, wenn Δx dem Werte Null zustrebt. Man drückt das so aus:

(gelesen limes für Δx=0 Δf/Δx) und um an diese Entstehung von f'(x) aus dem Differenzenquotienten zu erinnern, setzt man:

(3)

(gelesen df nach dx oder df durch dx), und nennt diesen Ausdruck auch den (ersten) Differentialquotienten von f(x) nach x. Die Größen dx und df, die Differentiale von x und f, sind ganz beliebig und nur an die Bedingung gebunden, daß ihr Quotient gleich f'(x) sein muß; es ist aber vorteilhaft, sich dx sehr klein zu denken, denn je kleiner dx ist, um so genauer stellt df = f'(x)dx den Zuwachs dar, den f(x) bekommt, wenn x um dx wächst. Vielfach denkt man sich dx und df auch als sogen. unendlich kleine Größen. Man sagt, eine Größe wird unendlich klein, wenn sie kleiner wird als jede noch so kleine Zahl: der Ausdruck »unendlich klein werden« ist aber nur eine abkürzende Ausdrucksweise, und man darf niemals sagen: eine Größe ist unendlich klein. Im Gegensatze dazu hat eine endliche Größe stets einen bestimmten Zahlenwert, und zwei endliche Größen, von denen sich beweisen läßt, daß ihre Differenz unendlich klein wird, also kleiner als jede noch so kleine Zahl, haben notwendig die Differenz Null, sind also einander gleich. Wird nun. Δx in diesem Sinn unendlich klein, so werden gleichzeitig auch Δf und φ(x, Δx) unendlich klein, der Quotient Δf/Δx unterscheidet sich daher unendlich wenig von der endlichen Größe f'(x). Deshalb kann man sagen: wird Δx unendlich klein, so wird ^Δf/_Δx gleich f'(x) und schreibt dafür ^df/_dx = f'(x), indem man sich dx und df unendlich klein denkt. Während also einer unendlich klein werdenden Größe kein bestimmter Wert zugeschrieben werden kann, da sie immer im Flusse begriffen ist, kann doch der Quotient zweier unendlich klein werdender Größen einen bestimmten endlichen Wert haben.

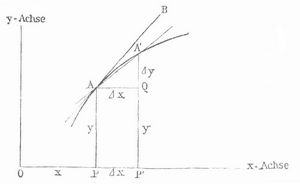
Deutet man x, y als rechtwinkelige Koordinaten (s.d.) in einer Ebene, bezogen auf zwei durch den Anfangspunkt O gehende senkrechte Achsen Ox und Oy, so stellt die Gleichung y = f(x) eine Kurve dar, und die Punkte A und A' mit den Koordinaten OP = x, PA = y und OP' = x+Δx, P'A' = y+Δy sind zwei Punkte dieser Kurve (s. Figur). Der Differenzenquotient ^Δy/_Δx = ^QA'/_AQ stellt die trigonometrische Tangente (s. Trigonometrie) des Winkels QAA' dar, also des Winkels, den die Verbindungslinie AA' der beiden Kurvenpunkte A und A' (die sogen. Sekante) mit der Achse Ox bildet.

Läßt man jetzt Δx immer kleiner werden, so rückt A' auf der Kurve dem Punkt A immer näher, und die Sekante AA' dreht sich um A, so daß sie der Geraden AB, welche die Kurve im Punkt A berührt (der sogen. Tangente der Kurve im Punkt A), immer näher kommt. Die Tangente AB ist also die Grenzlage, der die Sekante AA' zustrebt, wenn sich Δx der Null und also A' dem Punkt A immer mehr nähert. Da sich nun ^Δy/_Δx, wenn Δx der Null zustrebt, dem Grenzwert f'(x) = ^dy/_dx immer mehr nähert, so ist der Differentialquotient f'(x) nichts andres als die trigonometrische Tangente des Winkels, den die Kurventangente AB im Punkte x, y mit der x-Achse bildet. Auf diese Weise führt die Berechnung der Ableitung f'(x) einer Funktion f(x) zur Bestimmung der an die Karve y = f (x) im Punkt x, y gezogenen Tangente.

Will man den Differentialquotienten f'(x) einer Funktion f(x) berechnen oder, wie man sagt, die Funktion differentiieren, so kommt man bei einfachern Funktionen, wie x², 1/x, etc., zum Ziel, indem man die früher besprochene Zerlegung des Differenzenquotienten wirklich ausführt. Verwickeltere Funktionen setzt man aus einfachern zusammen, deren Differentialquotienten man schon berechnen kann. Ist f'(x) die Ableitung von f(x), so bezeichnet man die Ableitung von f'(x) mit f''(x) und nennt sie die zweite Ableitung oder den zweiten Differentialquotienten von f(x). Man schreibt auch

denkt man sich hier dx als eine unendlich klein werdende Größe, so ist d²f eine Größe, die unendlich klein wird wie dx² = dx.dx, die also im Vergleiche mit dx selbst unendlich klein wird, eine sogen. unendlich kleine Große zweiter Ordnung. Ähnlich bildet man Differentialquotienten dritter und noch höherer Ordnung von f(x). Man braucht diese z. B wenn man f(x) nach dem Taylorschen Satz (s.d.) in eine Potenzreihe entwickeln will.

Ist f(x,y) eine Funktion der zwei unabhängigen Veränderlichen x, y, so gibt es zwei Differentialquotienten[906] erster Ordnung, der eine wird erhalten, wenn man y als konstant betrachtet und f behandelt als wäre es eine Funktion von x allein, bei der Bildung des andern betrachtet man f als Funktion von y allein. Man nennt diese die partiellen Differentialquotienten von f und bezeichnet sie nach Jacobi mit δf/δx und δf/δy, benutzt also statt des d ein δ. Jeder von beiden ist wieder eine Funktion von x, y und besitzt daher zwei partielle Differentialquotienten, so daß aus f vier partielle Differentialquotienten zweiter Ordnung hervorgehen:

es läßt sich aber beweisen, daß hier die beiden mittlern Differentialquotienten einander gleich sind, daß es also für das Ergebnis gleichgültig ist, ob man zuerst nach x und dann nach y partiell differentiiert oder umgekehrt. Es gibt daher nur drei partielle Differentialquotienten zweiter Ordnung von f(x,y), die man mit

bezeichnet, ebenso nur vier von dritter Ordnung etc.

Die D. als allgemeines Rechnungsverfahren ist von Newton und bald nachher selbständig von Leibniz erfunden worden, obwohl viele spezielle Kunstgriffe, die im Grunde schon der D. angehören, bereits früher, besonders von Fermat, benutzt wurden, um Tangenten an Kurven zu ziehen und um Maxima und Minima von Funktionen zu berechnen (vgl. Maximum u. Minimum). Newton nannte die Differentiale Fluxionen, daher bezeichnet man die D. auch als Fluxionsrechnung. Die noch heute übliche praktische Schreibweise mit Differentialen stammt von Leibniz, durch den überhaupt die D. erst eine pädagogisch brauchbare Form erhalten hat, während Newton sie nur für seinen eignen Bedarf entwickelt hatte, ohne darauf bedacht zu sein, sie auf einfache Regeln zurückzuführen und sie dadurch auch für die Allgemeinheit der Mathematiker benutzbar zu machen. Die Begriffe Differential und unendlich kleine Größe sind lange die Ursache heftiger Streitigkeiten unter den Mathematikern gewesen und vielfach unklar oder ganz unrichtig erklärt worden; z. B. betrachtete Euler die Differential geradezu als Nullen. Lagrange wollte sie deshalb ganz vermeiden und führte zu diesem Zweck die Bezeichnung f'(x) und den Namen abgeleitete Funktion (fonction derivée) ein, die aber die Differentialbezeichnung nicht haben verdrängen können, zumal da man allmählich auch das Unendlichkleine richtig auffassen gelernt hat. Über die Geschichte der D. vgl. M. Cantor, Vorlesungen über Geschichte der Mathematik, Bd. 2 u. 3 (2. Aufl., Leipz. 1900–1902). Von Lehrbüchern der Differential- und Integralrechnung sind zu empfehlen die von Serret (deutsch von Harnack; neu bearbeitet von Bohlmann, Leipz. 1897 u. 1899, 2 Bde.), Czuber (das. 1898, 2 Bde.), Kiepert-Stegemann (1. Teil, 9. Aufl., Hannov. 1901; 2. Teil, 8. Aufl., das. 1903). Über die Anwendungen auf die Naturwissenschaften vgl. besonders das Lehrbuch von H. A. Lorentz (Leiden 1883; deutsch von Schmidt, Leipz. 1900); ferner Nernst u. Schoenflies, Einführung in die mathematische Behandlung der Naturwissenschaften (3. Aufl., Münch. 1901); Perry, Höhere Analysis für Ingenieure (deutsch von Fricke u. Süchting, Leipz. 1902). Durch Strenge der Beweise sind besonders ausgezeichnet: Genocchi-Peano, Differentialrechnung etc. (deutsch von Bohlmann u. Schepp, Leipz. 1899) u. Stolz, Grundzüge der D. und Integralrechnung (das. 1893–99, 3 Tle.).