Flächen [1]
[55] Flächen, zweidimensionale Gebilde, entweder eben oder krumm (vgl. Flächentheorie).
Geometrische Eigenschaften der Flächen.
Flächen, krumme. Eine krumme Fläche ist der geometrische Ort aller Lagen einer nach einem bestimmten Gesetze bewegten Kurve oder Fläche. Je nach der Art des Bewegungsgesetzes und der bewegten Linie oder Fläche, d.h. der Erzeugenden der Fläche, lassen sich die Flächen[55] einteilen; man kann unterscheiden: 1. Umdrehungsflächen; die Erzeugende ist eine Linie und dreht sich um eine beliebige Gerade im Räume als Achse. 2. Regelflächen; die Erzeugende ist eine gerade Linie; dabei ist die Fläche abwickelbar, wenn je zwei aufeinander folgende Lagen der bewegten Geraden in einer Ebene liegen, oder windschief, wenn dies nicht der Fall ist. 3. Umhüllungs- oder Rückungsflächen; die Erzeugende ist eine Fläche und bewegt sich nach einem bestimmten Gesetze. Vorstehende Unterscheidung schließt keineswegs aus, daß ein und dieselbe Fläche mehreren der obengenannten Gruppen zugleich angehört. Eine andre Einteilung der Flächen erfolgt nach ihrer algebraischen Ordnung, worunter man im allgemeinen die Anzahl der Schnittpunkte einer Geraden mit ihrer Oberfläche verlieht; ist diese Anzahl eine begrenzte, so heißt die Fläche algebraisch, im andern Falle transzendent.
Eine Fläche nter Ordnung besitzt als ebenen Schnitt stets eine Linie nter Ordnung. Legt man durch einen Punkt einer Fläche eine Anzahl Ebenen, ermittelt deren Schnitte mit der Fläche und konstruiert in dem genannten Punkte an die verschiedenen Schnittkurven der Tangenten, so bilden letztere im allgemeinen eine ebene Fläche, die Tangentialebene des. betreffenden Punktes an die Fläche; der gegebene Punkt selbst ist der Berührungspunkt der Tangentialebene mit der Fläche. Liegt der Punkt nicht auf der Fläche, so sind von ihm aus im allgemeinen unzählig viele Tangentialebenen an die Fläche möglich; sie bilden sämtlich eine Kegelfläche, welche die gegebene Fläche nach einer bestimmten Kurve berührt. Ist der gegebene Punkt eine Lichtquelle, so bildet die ebengenannte Kurve die Selbstschattengrenze der Fläche mit Bezug auf die genannte Lichtquelle. Fällt der Punkt in unendliche Ferne, so sind die sämtlichen ihn enthaltenden Tangentialebenen parallel zu einer Geraden und bilden eine die Oberfläche nach einer Kurve berührende Zylinderfläche. Genannte Kurve bezeichnet die Selbstschattengrenze der Fläche für den unendlich fernen Punkt als Lichtquelle. Durch die Punkte einer geraden Linie lassen sich nur eine begrenzte Anzahl von Tangentialebenen an die Fläche legen; sie bezeichnet, wenn die Fläche algebraisch ist, die Klasse der Fläche. Ist die Fläche abwickelbar, so ist eine Tangentialebene durch eine beliebig gegebene Gerade im allgemeinen nicht vorhanden; man versteht deshalb unter der Klasse einer abwickelbaren Fläche die Zahl der Tangentialebenen, die durch einen beliebigen Punkt an die Fläche möglich sind. Eine Tangentialebene schneidet eine Fläche nter Ordnung im allgemeinen noch nach einer Kurve nter Ordnung, die im Berührungspunkt der Tangentialebene mit der Fläche einen Doppelpunkt besitzt. Die beiden Tangenten in diesem Doppelpunkt haben mit der Fläche drei aufeinander folgende Punkte gemeinsam und heißen die zu dem Berührungspunkte gehörigen Haupt- oder Inflexionstangenten der Fläche. Diese Haupttangenten sind entweder beide wirklich vorhanden, der Punkt ist ein hyperbolischer Punkt der Fläche, oder sie fallen in eine Tangente zusammen, der Punkt ist parabolisch, oder sie sind endlich imaginär, der Punkt ist ein elliptischer Punkt der Fläche. Ist die Fläche eine Regelfläche, so ist jeder ihrer Punkte entweder hyperbolisch oder parabolisch, letzteres stets, wenn die Fläche abwickelbar ist.
Schneiden sich zwei algebraische Flächen von den Ordnungen n1 und n2, so ist ihr Schnitt im allgemeinen eine Raumkurve von der Ordnung n1 · n2. Berühren sich die Flächen in einem Punkte, so können sie sich außerdem noch nach einer Kurve von der Ordnung n1 · n2 schneiden, die im Berührungspunkte der beiden Flächen einen Doppelpunkt besitzt. Die Tangenten in diesem Doppelpunkte an die Schnittkurven liegen in der gemeinschaftlichen Tangentialebene beider Flächen; man erhält sie als Schnitt der gemeinsamen Tangentialebene mit einem Kegel, der den Berührungspunkt als Spitze und die Schnittlinie beider Flächen als Leitlinie besitzt. Drei Flächen von den Ordnungen n1, n2 und n3 schneiden sich nach einer Kurve von der Ordnung n1 · n2 · n3. – Eine Fläche nter Ordnung ist im allgemeinen durch (n + 1) (n + 2) (n + 3)/1 · 2 · 3 – 1 Ortsbedingungen, z.B. Punkte, vollständig bestimmt; eine Fläche zweiter Ordnung demnach durch 9 Punkte, eine Fläche dritter Ordnung durch 19 Punkte.
Literatur: S. unter Geometrie, darstellende.
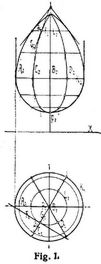
Umdrehungsfläche, entsteht durch Drehung einer ebenen Kurve A (s. Fig. 1 und 2) um eine in ihrer Ebene befindliche Gerade B als Drehungsachse. Eine zu letzterer senkrechte Ebene schneidet im allgemeinen die Fläche nach einer Kreislinie, die ein Parallelkreis der Drehungsfläche genannt wird. Alle die Drehungsachsen enthaltenden ebenen Schnitte sind kongruente Figuren und heißen Meridiane der Fläche, z.B. C, D (s. Fig. 1 und 2). Ist der Meridian eine algebraische Kurve von der Ordnung n, so ist die Drehungsfläche eine algebraische Fläche von der n ten Ordnung. Ist insbesondere die Meridiankurve eine Linie zweiter Ordnung und eine Hauptachse der letzteren die Drehungsachse, so entsteht eine Drehungsfläche zweiter Ordnung, und zwar die Kugel, das Ellipsoid, das Paraboloid und das Hyperboloid, je nachdem als Meridiankurve der Kreis, die Ellipse, Parabel oder Hyperbel in Betracht kommt.[56] Als Spezialfälle der Drehungsflächen zweiter Ordnung sind der senkrechte Kreiskegel bezw. Zylinder zu erwähnen; im ersten Falle besteht der Meridian aus zwei auf der Drehungsachse sich schneidenden Geraden, deren Winkel die letztere halbiert, im zweiten Falle bilden zwei parallele, gleich weit von der Drehungsachse abstehende Gerade den Meridianschnitt der Drehungsfläche.
Zur geometrischen Darstellung einer Drehungsfläche wählt man zweckmäßig eine Projektionsebene senkrecht zur Drehungsachse, die andre parallel zu einer Meridianebene; in diesem Fall besteht der Grundriß der Fläche entweder aus einer Kreis- oder Ringfläche, der Aufriß ist begrenzt durch einen Meridianschnitt (s. Fig. 1 und 2). Bei der obengenannten Annahme der Projektionsebenen projizieren sich die Aufrisse der Parallelkreise als Gerade senkrecht zur Drehungsachse, die Grundrisse als konzentrische Kreise. Die Meridiane stellen sich im Aufrisse als affine Kurven mit der Drehungsachse als Affinitätsachse, die Grundrisse als den Grundriß der Drehungsachse enthaltende Gerade dar (s. Fig. 1 und 2).
Tangentialebenen der Drehungsfläche. Die Tangentialebenen längs den Punkten eines Parallelkreises an eine Drehungsfläche bilden im allgemeinen einen senkrechten Kreiskegel, dessen Achse mit der Flächenachse zusammenfällt (s. Kreis L, Fig. 1); in speziellen Fällen kann der Kegel in einen Zylinder bezw. eine Ebene übergehen, und es heißt im ersten Falle der bezügliche Parallelkreis ein Aequator, z.B. die Kreise K und K' in Fig. 1 und 2; im letzteren Falle ein Polarkreis (s. die Kreise M und N in Fig. 2) bezw. ein Pol (s. Punkt p, Fig. 1) der Fläche. Längs den Punkten einer Meridiankurve bilden die Tangentialebenen an die Drehungsfläche eine Zylinderfläche, die zur Ebene der Meridiankurve senkrecht steht und die Drehungsfläche nach der Meridiankurve berührt. Soll in irgend einem Punkte a der Drehungsfläche (s. Fig. 1) eine Tangentialebene konstruiert werden, so zeichnet man durch diesen Punkt einen Parallelkreis sowie einen Meridian und an diese Kurven in dem gegebenen Punkte je eine Tangente F bezw. G; dann ist durch die beiden Tangenten F und G die Tangentialebene bestimmt.
Schnitt einer Ebene mit einer Drehungsfläche. Man denkt sich die Fläche durch Ebenen senkrecht zur Drehungsachse geschnitten; die Schnittlinien treffen die Drehungsfläche nach Parallelkreisen, die Ebene nach parallelen Geraden., Je ein Parallelkreis der Fläche und die in derselben Ebene liegende Gerade der Ebene treffen sich in Punkten der Schnittkurve zwischen Ebene und Drehungsfläche. Eine Tangente in einem Punkte an die Schnittkurve ergibt sich als Schnittlinie der Tangentialebene in dem betreffenden Punkte an die Fläche mit der Schnittebene.
Schnitt einer Geraden mit einer Drehungsfläche. Man legt durch die Gerade eine Ebene, bestimmt deren Schnitt mit der Drehungsfläche, die Schnittlinie trifft die Gerade in den gesuchten Schnittpunkten.
Schnitt zweier Drehungsflächen. Je nach der Lage der Achsen beider Flächen lassen sich drei Fälle unterscheiden; entweder sind die Achsen parallel oder sie schneiden sich oder sie sind windschief. Im ersten Falle schneidet man die beiden Drehungsflächen durch Ebenen senkrecht zu den Achsen beider Flächen und erhält in jeder Fläche als Schnittlinien Parallelkreise, die sich gegenseitig in Punkten der Schnittkurve beider Flächen begegnen; im zweiten Falle verwendet man als Hilfsflächen Kugeln, deren Mittelpunkte in den Schnittpunkt der beiden Achsen fallen. Diese Hilfskugeln treffen beide Flächen nach Parallelkreisen, deren Schnitte Punkte der Schnittkurve beider Drehungsflächen liefern. Bei windschiefer Lage der Achsen der Flächen schneidet man die beiden Flächen durch Ebenen, senkrecht zu einer der beiden Flächenachsen, und bestimmt die Schnittlinien der Hilfsebenen mit den beiden Flächen. Diese Schnittlinien treffen sich in Punkten der Schnittkurve beider Flächen.
Schnitt einer Drehungsfläche mit einer Zylinder- bezw. Kegelfläche. Man wählt auf der Drehungsfläche einen Parallelkreis, legt durch denselben eine zur Zylinderfläche parallele Zylinderfläche bezw. eine mit der gegebenen Kegelfläche konzentrische Kegelfläche. Die Schnittgeraden beider Zylinder- bezw. Kegelflächen schneiden auf dem angenommenen Parallelkreise Punkte der Durchschnittskurve beider Flächen aus. Sind andre als die bisher genannten Flächen mit einer Drehungsfläche zum Schnitt zu bringen, so wird man die beiden Flächen mit solchen Hilfsflächen schneiden, deren Schnittkurven mit den gegebenen Flächen sich am einfachsten konstruieren lassen. Die Tangente in einem Punkte der Schnittkurve zweier Flächen bestimmt sich als die Schnittlinie der Tangentialebenen in dem betreffenden Punkte an die beiden Flächen.
Tangentenkegel von einem Punkte außerhalb der Drehungsfläche an diese. Von einem Punkte außerhalb der Fläche sind an letztere unzählig viele Tangenten möglich, welche einen Kegel einschließen, der die Drehungsfläche nach einer Kurve berührt. Zur Konstruktion von Punkten dieser Kurve wählt man auf der Drehungsfläche einen beliebigen Parallelkreis, bestimmt den hierzu gehörigen, die Drehungsfläche berührenden Kegel und zeichnet an letzteren von dem gegebenen Punkte aus die möglichen Tangentialebenen; deren Berührungslinien liefern auf dem angenommenen Parallelkreis Punkte der Berührungskurve.
Tangentenzylinder parallel einer Geraden an eine Drehungsfläche. Man legt parallel zur gegebenen Richtung an eine Reihe von die Fläche nach Parallelkreisen berührenden Kegeln die möglichen Tangentialebenen; die Berührungslinien der letzteren mit den Kegeln liefern auf den zugehörigen Parallelkreisen Punkte der Berührungskurve.
Die zuletzt genannten Konstruktionen gewinnen eine praktische Bedeutung dann, wenn durch den gegebenen Punkt bezw. die gegebene Richtung eine Lichtquelle bestimmt ist, von der aus die Fläche eine Beleuchtung erfährt; in diesem Falle bezeichnet die Berührungskurve des Tangentenkegels durch den betreffenden Punkt bezw. des Tangentenzylinders parallel der gegebenen Richtung mit der Drehungsfläche die Selbstschattengrenze auf letzterer Fläche unter Voraussetzung zentraler bezw. paralleler Beleuchtung. (S.a. Schattenkonstruktionen sowie die unter Geometrie, darstellende, angegebene Literatur.)[57]
Flächen zweiter Ordnung. Unter einer Fläche zweiter Ordnung versteht man jede Fläche, die von einer Ebene nach einer Linie zweiten Grades, d.h. nach einem Kegelschnitte getroffen wird; hieraus folgt zugleich, daß es auf eine Fläche zweiter Ordnung keine andern ebenen Kurven als Kegelschnitte gibt. Ist auf einer Fläche zweiter Ordnung eine gerade Linie vorhanden, so wird jede durch die letztere gelegte Ebene die Fläche noch nach einer zweiten Geraden schneiden; es wird also die Fläche zweiter Ordnung eine Regelfläche sein.
Einige Polareigenschaften der Flächen zweiter Ordnung: Zieht man durch einen beliebigen Punkt des Raumes nach der Fläche zweiter Ordnung Sekanten und konstruiert für jede Sekante den zu dem gegebenen Punkte hinsichtlich der Durchschnittspunkte der Sekante mit der Oberfläche konjugierten vierten harmonischen Punkt, so liegen diese sämtlichen vierten harmonischen Punkte in einer Ebene, welche die Polarebene des Punktes hinsichtlich der Fläche zweiter Ordnung genannt wird. Der Punkt selbst heißt der zur Polarebene gehörige Pol. Schneidet die Polarebene die Fläche zweiter Ordnung nach einem Kegelschnitte, so bezeichnet man den zur Polarebene gehörigen Pol als außerhalb der Fläche liegend. Gehört der Pol der Fläche selbst an, so ist die zugehörige Polarebene die Tangentialebene der Fläche im Pole. Hat die Polarebene keinen reellen Kegelschnitt mit der Fläche zweiter Ordnung gemeinsam, so nennt man den zugehörigen Pol innerhalb der Fläche liegend. Verbindet man die Schnittpunkte der Polarebene mit der Fläche zweiter Ordnung mit dem zugehörigen Pole, so sind diese Verbindungslinien Tangenten an die Oberfläche zweiter Ordnung und bilden den zu dem Punkte gehörigen Tangentenkegel an die Fläche zweiter Ordnung. Ist der betreffende Punkt eine Lichtquelle, so ist die Berührungskurve des Tangentenkegels mit der Oberfläche die Selbstschattengrenze der Fläche zweiter Ordnung hinsichtlich des gewählten Punktes als Lichtquelle. Für eine Fläche zweiter Ordnung ist daher bei zentraler Beleuchtung die Selbstschattengrenze stets ein Kegelschnitt, desgleichen ihre Schlagschattengrenze auf eine gegebene ebene Fläche. Fällt die Spitze des Tangentenkegels in unendliche Ferne, so geht der Tangentenkegel in einen Tangentenzylinder über, der die Fläche nach einem Kegelschnitte berührt, dessen Mittelpunkt zugleich der Mittelpunkt der Fläche genannt, wird und die Eigenschaft hat, daß sämtliche durch ihn gehenden Sehnen in ihm halbiert werden. Jede den Mittelpunkt enthaltende Ebene heißt eine Durchmesserebene, jede den Mittelpunkt enthaltende Sehne ein Durchmesser der Fläche zweiter Ordnung. Ist der unendlich ferne Punkt eine Lichtquelle, so ist die Berührungskurve des Tangentenzylinders mit der Fläche zweiter Ordnung die Selbstschattengrenze; diese ist somit unter Voraussetzung einer Beleuchtung durch parallele Lichtstrahlen für eine Fläche zweiter Ordnung stets ein den Mittelpunkt der Fläche als Mittelpunkt besitzender Kegelschnitt.
Durch eine beliebige Gerade lassen sich im allgemeinen nur zwei Tangentialebenen an eine Fläche zweiter Ordnung legen; die Fläche zweiter Ordnung ist daher auch eine Fläche zweiter Klasse oder kurzweg eine Fläche zweiten Grades. Die Verbindungslinie der Berührungspunkte der die gegebene Gerade Q enthaltenden Tangentialebenen liefern eine Gerade G1, durch welche die Polarebenen für sämtliche Punkte von G hindurchgehen. Zwei solche Gerade G, G1 heißen konjugierte Polaren der Fläche zweiten Grades. Liegt die Gerade G in Unendlicher Ferne, so geht die zu G konjugierte Polare G1 durch den Mittelpunkt des Kegelschnittes und man nennt die die Gerade G enthaltende Durchmesserebene die zu G1 konjugierte Durchmesserebene. Wählt man in letzterer irgend zwei konjugierte Durchmesser des in ihr liegenden Kegelschnittes, so bilden diese mit G1 drei konjugierte Durchmesser der Fläche zweiten Grades und die durch sie bestimmten Ebenen drei konjugierte Durchmesserebenen der Fläche. Sie haben die Eigenschaft, daß die Ebene von je zwei Durchmessern die Polarebene des unendlich fernen Punktes des dritten Durchmessers darstellt. – Stehen drei konjugierte Durchmesser einer Fläche zweiten Grades aufeinander senkrecht, so heißen sie die Hauptachsen der Fläche; die durch sie bestimmten Ebenen sind die Hauptachsenebenen und die in ihnen liegenden Kegelschnitte die Hauptachsenschnitte der Fläche.
Durch irgend zwei ebene Schnitte einer Fläche zweiten Grades lassen sich im allgemeinen stets zwei Kegelflächen zweiten Grades legen, deren Spitzen auf der zur Schnittlinie der beiden Ebenen konjugierten Polaren liegen; hieraus folgt, daß parallele Ebenen eine Fläche zweiten Grades nach ähnlichen und ähnlich liegenden Kegelschnitten schneiden, eine Eigenschaft, die für konstruktive Zwecke nützlich verwendet werden kann. Zwei Flächen zweiten Grades schneiden sich im allgemeinen nach einer Linie vierter Ordnung, die insbesondere in zwei Kegelschnitte zerfallen kann; dies ist der Fall, wenn die Flächen zweiten Grades sich in zwei Punkten berühren. Ist eine der beiden Flächen eine Kugel und findet eine Berührung in zwei Punkten statt, so besteht die Schnittkurve aus zwei Kreisen. Es gibt somit für jede Fläche zweiten Grades zwei Lagen von Ebenen, welche die Fläche nach Kreisen schneidet. Findet die Berührung nur in einem Punkte statt, so ist die Schnittkurve beider Flächen eine Kurve vierter Ordnung mit einem Doppelpunkte. Sind die Flächen zweiten Grades Regelflächen und haben dieselben eine Erzeugende gemeinsam, so besteht der übrige Schnitt aus einer Kurve dritter Ordnung.
Einteilung der Flächen zweiten Grades. Nach der Gestalt der Hauptachsenschnitte unterscheidet man folgende Flächen zweiten Grades:
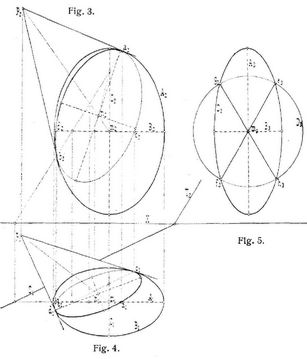
1. Das Ellipsoid. Die drei Hauptachsenschnitte sind Ellipsen A, B, C (s. Fig. 3–5); ist einer der Hauptachsenschnitte ein Kreis, so sind die beiden andern kongruente Ellipsen und man erhält das Umdrehungsellipsoid; es entsteht durch Umdrehung einer Ellipse um eine ihrer Hauptachsen. Findet die Drehung um die große Achse statt, so entsteht das Umdrehungsellipsoid erster Art oder das bifokale Ellipsoid; alle Meridiane besitzen die nämlichen Brennpunkte und es kann das Ellipsoid auch definiert werden als der geometrische Ort aller Punkte im Räume, die von zwei festen Punkten eine gegebene Abstandssumme besitzen. – Findet die Drehung um die kleine Ellipsenachse statt, so entsteht das Umdrehungsellipsoid[58] zweiter Art oder das Sphäroid; die Brennpunkte der Meridianellipse beschreiben einen Kreis, den Fokalkreis des Sphäroides; man erhält die Brennpunkte der übrigen Meridianellipsen im Durchschnitte ihrer Ebenen mit dem Fokalkreise des Sphäroides. Beim Ellipsoid ist die Berührungskurve eines Tangentenkegels bezw. eines Tangentenzylinders stets eine Ellipse bezw. ein Kreis. Sind alle Hauptachsenschnitte Kreise, so entsteht als Fläche die Kugel. Bei der Darstellung des Ellipsoides durch Projektion wählt man die Projektionsebenen zweckmäßig parallel zu den Achsenebenen; dann stellen die Achsenschnitte zugleich die Umrisse oder Konturen der Fläche für die bezüglichen Projektionsebenen dar. – Für das in Fig. 3–5 gezeichnete Ellipsoid ist die Konstruktion der Berührungskurve des von dem Punkt p an die Oberfläche gelegten Tangentenkegels angedeutet. Die Tangenten von den Projektionen p1 und p2 an die zugehörigen Umrisse der Flächen geben für jede Projektion der Berührungskurve zwei Tangenten mit ihren Berührungspunkten. Da außerdem der Mittelpunkt des Berührungskegelschnittes sich als Schnittpunkt der Verbindungslinie des Punktes p mit dem Mittelpunkte des Ellipsoides bestimmt, so kennt man von Grund- und Aufriß des Berührungskegelschnittes je den Mittelpunkt sowie zwei Tangenten mit ihren Berührungspunkten, und es unterliegt nach der Lehre von den Kegelschnitten keiner Schwierigkeit, die Hauptachsen der Projektionen des Berührungskegelschnittes zu bestimmen und diesen selbst punktweise zu konstruieren. Die Ebene der Berührungskurve ist, wie schon früher erwähnt, die Polarebene des Punktes p. Mit vorstehendem ist auch die Aufgabe gelöst, den Schnitt einer beliebigen Ebene S1 T2 mit dem Ellipsoid zu konstruieren. Man hat nur nötig, die Schnittlinien cd und ab der Ebene S1 T2 mit der Ebene des ersten und zweiten Umrisses zu ermitteln und in den Schnittpunkten c1 d1 a2 b2 dieser Linien mit den zugehörigen Umrißkurven die Tangenten an letztere zu zeichnen. Hierdurch bestimmt sich der Pol p der Ebene S1 T2 und die Aufgabe ist auf die vorhergehende zurückgeführt. In Fig. 5 ist außerdem die Lage der Kreisschnittebenen des Ellipsoides bestimmt; die Projektion D3 einer Kugel mit m3 als Mittelpunkt und einem Halbmesser gleich der mittleren Hauptachse des Ellipsoides schneidet die Ellipse C3 in den Punkten e3f3 und g3 h3. Die Verbindungslinien e3 f3 und g3 h3 stellen die dritten Projektionen zweier Ebenen dar, die aus dem Ellipsoide Kreise ausschneiden.
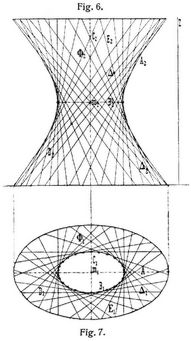
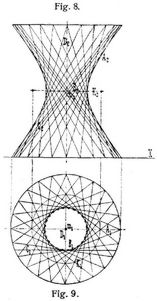
2. Das einschalige oder windschiefe Hyperboloid. Zwei der Hauptachsenschnitte sind Hyperbeln (s. Fig. 6), deren gemeinsame imaginäre Achse die eine Hauptachse der Fläche bildet, der dritte Achsenschnitt ist eine Ellipse C (s. Fig. 7), die Fläche ist eine Regelfläche und kann auch hervorgebracht werden durch Bewegung einer geraden Linie D, die stets drei vorgegebene Gerade Δ, E und Φ (s. Fig. 6 und 7) schneidet. Geht der elliptische Achsenschnitt in einen Kreis über, so entsteht das einschalige Umdrehungshyperboloid (s. Fig. 8 und 9). Dasselbe kann in doppelter Weise hervorgebracht werden, einmal durch Drehung einer Hyperbel um ihre imaginäre Achse D oder aber durch Drehung einer geraden Linie C um eine zweite, zur ersten windschief liegende Gerade D als Achse. Die Fläche besitzt einen Fokalkreis K, den Ort der Brennpunkte der[59] Meridianhyperbeln; sind die Meridianhyperbeln gleichseitig, so erhält man das gleichseitige Hyperboloid.
3. Das zweischalige Hyperboloid. Zwei Achsenschnitte sind Hyperbeln A und B (s. Fig. 10 und 11), deren gemeinsame reelle Achse eine Hauptachse der Fläche bildet; die dritte Hauptachsenebene enthält keinen reellen Kegelschnitt, doch liefern Parallelschnitte zur dritten Achsenebene ähnliche und ähnlich liegende Ellipsen (in Fig. 12 ist der Schnitt der Fläche mit der Projektionsebene E1 als Ellipse C1 gezeichnet); gehen letztere in Kreise über, so entsteht das zweischalige Umdrehungshyperboloid. Es kann aufgefaßt werden als der geometrische Ort aller Punkte im Räume, die von zwei gegebenen Punkten eine gegebene Abstandsdifferenz besitzen. Die sämtlichen Meridianhyperbeln besitzen dieselben Brennpunkte, weshalb die Fläche auch als bifokales Hyperboloid bezeichnet wird.
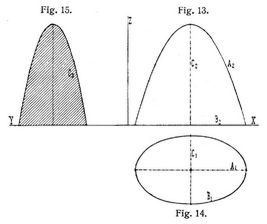
4. Das elliptische Paraboloid. Zwei Hauptachsenschnitte (s. Fig. 13 und 15) sind Parabeln A und C, alle zur dritten Achsenebene parallelen Schnitte ähnliche und ähnlich liegende Ellipsen. Der Schnitt mit der Projektionsebene E1 ist in Fig. 14 als Ellipse B1 dargestellt. Der Mittelpunkt der Fläche liegt in unendlicher Ferne. Werden die zuletzt genannten Schnitte kreisförmig, so entsteht das Umdrehungsparaboloid; es wird hervorgerufen durch Umdrehung einer Parabel um ihre Achse und kann aufgefaßt werden als der geometrische Ort aller Punkte im Räume, die von einem festen Punkte, dem Brennpunkt der Meridianparabel, und einer festen Ebene, der durch die Leitlinie der Parabel senkrecht zur Parabelachse gelegten Ebene, gleichen Abstand besitzen.
5. Das hyperbolische oder windschiefe Paraboloid. Zwei Achsenschnitte sind Parabeln A und B (s. Fig. 16 und 17), alle zur dritten Achsenebene parallelen Schnitte sind ähnliche und ähnlich liegende Hyperbeln; der Schnitt mit der Projektionsebene E1 ist als Hyperbel C1 gezeichnet. Die Fläche ist eine Regelfläche und kann auch hervorgerufen werden durch Bewegung einer geraden Linie, die stets parallel zu einer gegebenen Ebene bleibt und außerdem in jeder ihrer Lagen zwei vorgegebene gerade Linien schneidet. Bei der gewählten Darstellung kann die erwählte Ebene parallel zu einer der Asymptoten der Hyperbel C gewählt werden. Es sind demnach zwei solcher Ebenen vorhanden, zu denen die Erzeugenden des Paraboloides bezw. parallel sind, d.h. es gibt auf dem Paraboloide zwei Systeme von Erzeugenden, das eine System ist parallel zur Ebene D1, das andre zur Ebene E1.
Aus den fünf vorgenannten Arten von Flächen zweiten Grades leiten sich noch als Spezialfälle die Kegel- und Zylinderflächen zweiten Grades ab; die Kegelfläche zweiten Grades entsteht aus dem Hyperboloide, wenn statt der Hyperbeln deren Asymptoten als Achsenschnitte gewählt werden. Die Zylinderfläche zweiten Grades entsteht aus dem Paraboloide, wenn statt der parabolischen Achsenschnitte je ein Paar paralleler Geraden als solche gewählt werden.
Die unter 1., 3., 4. aufgeführten Flächen zweiten Grades führen die gemeinsame Bezeichnung »elliptische Flächen zweiten Grades«, weil sie in bestimmter Weise durch räumlich kollineare Verwandlung aus der Kugel abgeleitet werden können, indem das räumlich zentrisch kollineare Abbild einer Kugelfläche eine dieser Flächen sein kann (s. Zentralprojektion). Die unter 2. und 5. genannten Flächen sind die windschiefen Flächen zweiten Grades, während die Kegel- und Zylinderflächen zweiten Grades die abwickelbaren Flächen zweiten Grades bilden. Vgl. a. die analytische Darstellung in Flächen zweiten Grades.
Literatur: S. unter Geometrie, darstellende.
[60] Erzeugung einer abwickelbaren Fläche. Bewegt sich ein Punkt im Räume nach einem bestimmten Gesetze, so entsteht eine Raumkurve. Die sämtlichen Tangenten einer Raumkurve bilden ihre Tangentenfläche und diese ist eine abwickelbare (developpable) Fläche, weil es möglich ist, die von aufeinander folgenden Tangenten gebildeten Flächenstreifen, Flächenelemente, durch Drehung um die je zwei Streifen gemeinsame Kante ohne Aenderung der Form der Elemente, d.h. ohne Faltung, in eine einzige Ebene auszubreiten (abzuwickeln). Die Tangenten der Raumkurve sind Mantellinien oder Erzeugende der abwickelbaren Fläche. Die gleiche Fläche kann auch hervorgebracht werden durch Bewegung einer Ebene. Je zwei aufeinander folgende Ebenen schneiden sich nach Geraden, die wieder als Mantellinien oder Erzeugende der Fläche bezeichnet werden und gleichfalls als Tangenten eine Raumkurve einhüllen. Zu jeder Raumkurve gehört eine abwickelbare Fläche als Tangentenfläche, zu jeder abwickelbaren Fläche eine Raumkurve als Rückkehrkante. Zwei aufeinander folgende Tangenten der Raumkurve enthalten von letzterer drei aufeinander folgende Punkte, und die Ebene dieser Punkte ist eine Schmiegungs- oder Oskulationsebene der Raumkurve. Die zu einer Raumkurve gehörige abwickelbare Fläche ist die Fläche der Schmiegungsebenen der Kurve. Jede solche Schmiegungsebene enthält zwei aufeinander folgende Erzeugende der abwickelbaren Fläche, d.h. sie berührt die Fläche nach dieser Erzeugenden und ist eine Tangentialebene der abwickelbaren Fläche. Ihr Schnitt mit einer beliebigen Ebene ist eine Tangente an die Schnittkurve dieser Ebene mit der abwickelbaren Fläche. Hierdurch hat man ein Mittel, die Tangentialebene an eine abwickelbare Fläche in einem gegebenen Punkte der Fläche zu konstruieren. Man zieht durch den Punkt eine Erzeugende der Fläche und ermittelt deren Schnittpunkt mit einer beliebigen auf der Fläche liegenden ebenen Kurve. Die Tangente an letztere bestimmt mit der Erzeugenden durch den gegebenen Punkt die Tangentialebene in diesem. Zwei aufeinander folgende Erzeugende bezw. Tangentialebenen einer abwickelbaren Fläche bilden je einen unendlich kleinen Winkel; der erstere heißt Kontingenzwinkel, der letztere Torsions- oder Windungswinkel.
Krümmung einer Raumkurve. Liegt auf einer abwickelbaren Fläche eine beliebige Kurve und ist ab ein unendlich kleines Bogenstück desselben, zu welchem der Kontingenzwinkel Θ und der Torsionswinkel η gehört, so bezeichnet man das Verhältnis a b/Θ = 1/ρ1 als die erste, das Verhältnis a b/η = 1/ρ2 als die zweite Krümmung des Kurvenelementes. Durch drei aufeinander folgende Punkte der Kurve geht ein Krümmungskreis, vier aufeinander folgende Punkte liegen auf der Oberfläche der Schmiegungskugel.
Haupt- und Binormale einer Raumkurve. Errichtet man in einem Punkte a einer Raumkurve K zur zugehörigen Tangente eine Normalebene, so lassen sich in letzterer durch a unzählig viele Normalen zur Kurve K. ziehen; eine davon liegt in der Schmiegungsebene und heißt die Hauptnormale, eine andre steht senkrecht hierzu und führt die Bezeichnung Binormale.
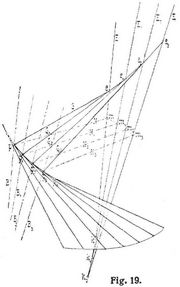
Evolutenfläche der Raumkurve. Aufeinander folgende Normalebenen einer Raumkurve umhüllen eine abwickelbare Fläche, die Evolutenfläche der ersteren; ihre Erzeugenden sind parallel zu den Binormalen der Raumkurve und schneiden sich in der Rückkehrkurve der Evolutenfläche, dem Ort der Mittelpunkte k der Schmiegungskugeln der Raumkurve (Fig. 19). Die Tangenten- und Evolutenfläche einer Raumkurve haben eine krumme Linie gemeinsam, den Ort der Krümmungsmittelpunkte m der Raumkurve. Jedem Punkte p der Raumkurve entspricht eine bestimmte zur Binormale des Punktes p parallele Erzeugende E der Evolutenfläche. Zieht man von p nach einem beliebigen Punkte e von E eine Gerade G, so ist G eine Normale zur Raumkurve K und schneidet die zu E benachbarte Erzeugende E1 in einem Punkte e1 durch den wieder eine Normale G1 zu K gezogen werden kann, die E2 in e2 schneidet u.s.w. Die Linien G sind Normalen zur Kurve K und Tangenten an die Kurve der e. Letztere Kurve ist somit eine Evolute von K. Zu einer Raumkurve K gehören unendlich viele Evoluten, die alle auf der Evolutenfläche von K liegen.
Evolventenfläche einer Raumkurve. Bewegt man eine Tangente ohne Gleiten längs einer Raumkurve, so beschreibt jeder Punkt der Tangente bei dieser Bewegung eine Evolvente der Raumkurve. Zu einer Raumkurve gehören unendlich viele Evolventen, die alle auf der Tangentenfläche der Raumkurve liegen; erstere ist somit auch die Evolventenfläche der letzteren.
Krümmungslinien der abwickelbaren Flächen. Die Evolventen einer Raumkurve sind Linien auf ihrer abwickelbaren Fläche, deren Normalen in aufeinander folgenden Punkten sich schneiden. Das gleiche ist der Fall hinsichtlich der Normalen längs den Punkten der Erzeugenden der abwickelbaren Fläche. Diese beiden Systeme von Linien, die sich überall rechtwinklig durchschneiden, nennt man die Krümmungslinien der abwickelbaren Fläche.
Asymptoten- oder Richtungskegel der abwickelbaren Fläche. Zieht man durch einen beliebigen Punkt des Raumes zu allen Erzeugenden der abwickelbaren Fläche Parallellinien, so bilden letztere die Mantelfläche eines Kegels, welche der Asymptoten- oder Richtungskegel der abwickelbaren Fläche heißt. Seine Tangentialebenen sind parallel zu denen der abwickelbaren Fläche.[61]
Tangentialebene einer abwickelbaren Fläche bei nicht gegebenem Berührungspunkt. Soll von einem Punkte außerhalb der Fläche eine Tangentialebene an die Fläche konstruiert werden, so legt man im allgemeinen durch den Punkt eine Ebene, ermittelt deren Schnitt mit der Fläche und zeichnet an die Schnittkurve durch den gegebenen Punkt die möglichen Tangenten; die Erzeugenden durch deren Berührungspunkte bestimmen mit den zugehörigen Tangenten die möglichen Tangentialebenen. Liegt der Punkt in unendlicher Ferne auf einer gegebenen Geraden, so legt man parallel zu der letzteren an den Richtungskegel die möglichen Tangentialebenen (s. Kegelfläche) und ermittelt die zu diesen parallelen Tangentialebenen der abwickelbaren Fläche. Ist der gegebene Punkt, gleichviel ob er in endlicher oder unendlicher Ferne sich befindet, eine Lichtquelle, von der aus die Fläche Licht erhält, so begrenzen die Berührungslinien der von dem Punkte an die Fläche gelegten Tangentialebenen den Selbstschatten (s. Schattenkonstruktionen) auf der Fläche [1].
Abwicklung des Mantels einer abwickelbaren Fläche in eine Ebene. Bei der Entwicklung einer abwickelbaren Fläche bleiben alle Winkel und Längen auf der Fläche ungeändert. Die Erzeugenden bilden also vor und nach der Abwicklung unter sich und mit irgend einer auf der Fläche liegenden Kurve die nämlichen Winkel. Anders verhält es sich hinsichtlich der Krümmung einer Kurve. Sind (s. Fig. 20) a b c drei aufeinander folgende Punkte einer auf einer abwickelbaren Fläche liegenden Kurve, so geht durch die Punkte a, b, c, ein Krümmungskreis der Kurve. Wird nun das Flächenelement BC in die Ebene AB um die Kante B gedreht, so beschreibt C einen senkrechten Kreiskegel mit B als Achse und m als Mittelpunkt. Da nun aber der Winkel η als unendlich klein angenommen werden kann, so ist Winkel bc'c ein rechter, d.h. man erhält bc' als Projektion von bc in die Ebene AB. Projiziert man den ganzen Krümmungskreis K in die Ebene AB, so ergibt sich als Projektion eine Ellipse, deren Krümmungskreis im Punkte b den Krümmungskreis für die Abwicklung der Kurve K darstellt. Sind nun ρ und ρn die Krümmungshalbmesser vor und nach der Abwicklung und bezeichnet W den Winkel der Tangentialebene mit der Ebene des Krümmungskreises im fraglichen Punkte, so ist die kleine Achse der Ellipse, die als Projektion des Krümmungskreises in die Tangentialebene AB sich ergibt, gleich 2 ρ · cos W; für den Endpunkt der kleinen Achse ist aber der Krümmungshalbmesser ρn = ρ2/ρ · cos W = ρ/cos W. Für W = Q erhält man ρ = ρn, W = 90° ist ρn = ∞. Das erste ist der Fall für alle Punkte der Rückkehrkante einer abwickelbaren Fläche, woraus folgt, daß für die Rückkehrkante einer abwickelbaren Fläche die Krümmung durch die Abwicklung des Flächenmantels in eine Ebene ungeändert bleibt. Steht die Tangentialebene eines Punktes einer Kurve auf der zugehörigen Schmiegungsebene des Kurvenpunktes senkrecht, so erhält die Kurve nach der Abwicklung in dem entsprechenden Punkte einen Wende- oder Inflexionspunkt. Zeichnet man auf der abgewickelten Fläche eine Linie mit lauter Wendepunkten, d.h. eine Gerade, so entspricht derselben auf der Fläche eine Linie, deren sämtliche Schmiegungsebenen auf den zugehörigen Tangentialebenen senkrecht stehen; sie heißt eine geodätische Linie und ist die kürzeste Verbindungslinie zwischen zwei Punkten der Fläche.
Rektifizierende abwickelbare Fläche einer Raumkurve. Legt man durch sämtliche Tangenten und die zugehörigen Binormalen einer Raumkurve Ebenen, so bilden letztere eine abwickelbare Fläche, deren Tangentialebenen auf den entsprechenden Schmiegungsebenen der Raumkurve senkrecht stehen; letztere ist somit eine geodätische Linie dieser abwickelbaren Fläche und verwandelt sich bei der Abwicklung der letzteren in eine gerade Linie.
Algebraische abwickelbare Flächen und Raumkurven. Eine Raumkurve heißt algebraisch, wenn sie von einer Ebene in einer endlichen Anzahl von Punkten geschnitten wird, im Gegensatz zu einer transzendenten Raumkurve, deren Schnittpunkte mit einer Ebene unzählig viele sein können. Die Tangentenfläche einer algebraischen Raumkurve ist eine algebraische abwickelbare Fläche, sie wird von einer Geraden in einer endlichen Anzahl von Punkten getroffen.
Charaktere einer Raumkurve bezw. deren abwickelbarer Fläche. Man unterscheidet bei einer Raumkurve 1. ihre Ordnung, d.i. die Anzahl ihrer Schnittpunkte mit einer beliebigen Ebene, 2. ihren Rang, d.i. die Anzahl der Schnittpunkte ihrer Tangenten mit einer beliebigen Geraden, 3. ihre Klasse, d.i. die Anzahl der Schmiegungsebenen, die durch einen beliebigen Punkt des Raumes gehen. Bei einer abwickelbaren Fläche unterscheidet man ebenso 1. ihre Ordnung, sie ist gleich der Ordnung eines ebenen Schnittes der Fläche und gleich der Anzahl Schnittpunkte der Schnittkurve mit einer beliebigen Geraden ihrer Ebene – mit andern Worten: Die Ordnung einer abwickelbaren Fläche ist gleich dem Range ihrer Rückkehrkante –; 2. ihre Klasse, sie ist gleich der Klasse eines ebenen Schnittes der Fläche und gleich der Anzahl Tangenten an die Schnittkurve von einem Punkte ihrer Linie. Die Klasse der abwickelbaren Fläche ist gleich der Klasse ihrer Rückkehrkante.
Singularitäten der Raumkurve und ihrer abwickelbaren Fläche. Bei der Entstehung der Raumkurve und ihrer abwickelbaren Fläche durch Bewegung eines Punktes bezw. einer Ebene können folgende Singularitäten auftreten: Der bewegliche Punkt bezw. die Ebene hält einen Augenblick in der Bewegung inne und kehrt die Bewegungsrichtung um; es entsteht im ersten Falle ein stationärer Punkt (s. Fig. 21), d.h. ein Rückkehrpunkt der Raumkurve, im zweiten Falle aber eine stationäre Schmiegungsebene der Kurve bezw. eine stationäre Tangentialebene der Fläche (s. Fig. 22). Außerdem unterscheidet man stationäre [62] Tangenten, d.h. solche Tangenten, die drei unmittelbar aufeinander folgende Punkte enthalten (Fig. 23), Doppelpunkte, Doppelschmiegungs- bezw. Tangentialebenen, für die entweder der bewegliche Punkt oder die bewegliche Ebene zweimal durch dieselbe Stelle des Raumes hindurchgeht, endlich Doppeltangenten der Raumkurve oder Doppelerzeugende der Fläche, d.h. Linien, welche die Raumkurve in zwei verschiedenen Punkten berühren. Außer den Doppelelementen kann eine Raumkurve bezw. abwickelbare Fläche auch noch mehrfache Elemente besitzen, z.B. k fache Elemente, d.h. k fache Punkte, Tangenten, Schmiegungsebenen.
Zusammenhang einer Raumkurve mit ihrer Projektion auf einer Ebene. Eine Raumkurve nter Ordnung hat als Projektion im allgemeinen eine Kurve nter Ordnung, denn erstere hat mit jeder projizierenden Ebene n Punkte gemeinsam; dieselbe Anzahl gemeinsamer Punkte besitzt aber auch die Spur der projizierenden Ebene mit der Projektion der Raumkurve. Die Klasse der Projektion ist gleich dem Range der Raumkurve, denn jede Tangente von einem beliebigen Punkte p der Projektionsebene ist die Projektion einer Tangente der Raumkurve, die den Projektionsstrahl durch p enthält. Die Ordnung bezw. Klasse der Projektion vermindert sich um eine Einheit, wenn das Projektionszentrum auf der Kurve bezw. auf einer Tangente der Kurve liegt.
Singularitäten der ebenen Projektion einer Raumkurve. Den Singularitäten einer Raumkurve entsprechen gewisse Singularitäten ihrer ebenen Projektion. Letztere besitzt so viele Rückkehrpunkte, als die Raumkurve stationäre Punkte hat (s. Fig. 21); außerdem erzeugt noch jede Tangente der Raumkurve, die das Projektionszentrum enthält, einen Rückkehrpunkt. Ist also ß die Anzahl der stationären Punkte der Raumkurve und gehen ρ Tangenten durch das Zentrum, so besitzt die Projektion ß + ρ Rückkehrpunkte. Die Anzahl der stationären Tangenten der Projektion ist gleich der Anzahl der stationären Tangenten der Raumkurve (s. Fig. 23), außerdem erzeugt jede das Projektionszentrum enthaltende Schmiegungsebene eine weitere stationäre Tangente der Projektion. Ist also H die Anzahl der stationären Tangenten der Raumkurve und gehen m Schmiegungsebenen durch das Projektionszentrum, so ist die Anzahl der stationären Tangenten der Projektion m + H. Jedem Doppelpunkte der Raumkurve entspricht ein Doppelpunkt der Projektion; außerdem erzeugt aber jeder die Kurve zweimal schneidende Projektionsstrahl einen Doppelpunkt der Projektion. Ist also D die Anzahl der Doppelpunkte der Raumkurve und schneiden h Projektionsstrahlen die Kurve doppelt, so besitzt die Projektion D + h Doppelpunkte. Jeder Doppeltangente der Raumkurve entspricht eine Doppeltangente der Projektion, ebenso erzeugt jede die Fläche doppelt berührende projizierende Ebene eine Doppeltangente der Projektion. Ist d die Anzahl der Doppeltangenten der Raumkurve und berühren y projizierende Ebenen die Kurve doppelt, so hat die Projektion d + y Doppeltangenten.
Singularitäten eines ebenen Schnittes einer abwickelbaren Fläche. Ein ebener Schnitt einer abwickelbaren Fläche besitzt Singularitäten, und zwar Rückkehrpunkte: Jeder Schnittpunkt der Rückkehrkante der Fläche mit der Schnittebene wird ein Rückkehrpunkt der Schnittkurve, desgleichen jeder Schnittpunkt mit einer stationären Erzeugenden der Fläche (s. Fig. 23). Die Gesamtzahl der Rückkehrpunkte eines ebenen Schnittes ist also gleich n + Θ, n die Ordnung der Rückkehrkante und Θ die Anzahl ihrer stationären Tangenten. Stationäre oder Wendetangenten: Die Spur jeder stationären Tangentialebene der Fläche gibt eine stationäre Tangente der Schnittkurve (s. Fig. 23), ihre Gesamtzahl ist gleich α. Doppelpunkte: Gehen durch einen Punkt der Schnittkurve zwei Erzeugende der Fläche, so ist derselbe ein Doppelpunkt der Schnittkurve, außerdem gibt die Spur einer jeden Doppelerzeugenden der Fläche einen Doppelpunkt der Schnittkurve. Die Gesamtzahl ist x + d, x die Anzahl der erstgenannten Punkte, d die Zahl der Doppelerzeugenden der Fläche. Doppeltangenten: Die Spur jeder Doppeltangential- oder Schmiegungsebene gibt eine Doppeltangente der Schnittkurve; sind außerdem in der Schnittebene noch g Gerade vorhanden, durch die je zwei Tangentialebenen an die Fläche möglich sind, so ist die Anzahl der Doppeltangenten der Schnittkurve gleich Δ + g, Δ die Anzahl der Doppeltangentialebenen. Der Schnittkurve kommen überdies noch unendlich ferne Punkte zu, wenn nämlich Erzeugende der Fläche parallel zur Schnittebene gerichtet sind. Die Kurve hat dann Asymptoten; man erhält sie als Schnittlinien der Tangentialebenen in den unendlich fernen Punkten mit der Schnittebene. Zwischen den Charakteren n, m, r, x, y, h, g, α und ß bestehen die folgenden, nach ihrem Entdecker Cayley benannten sechs Gleichungen:
1. r = n (n – 1) – 2 h – 3 ß
2. n = r (r – 1) – 2 y – 3 m
3. m – ß = 3 (r – n)
4. m = r (r – 1) – 2 x – 3 n
5. r = m (m – 1) – 2 g – 3 α
6. α – n = 3 (m – r).
[63] Sind von den Charakteren der Raumkurve drei beliebig, jedoch mit Ausnahme der Zusammenstellung r, x, ß oder r, y, a gegeben, so lassen sich die übrigen sechs mit Hilfe der obenstehenden Gleichungen ermitteln.
Geschlecht einer Raumkurve. Hierunter versteht man die Beziehungen
p = 1/2 (n – 1) (n – 2) – h – ß
p = 1/2 (r – 1) (r – 2) – y – r
p = 1/2 (r – 1) (r – 2) – x – n
p = 1/2 (m – 1) (m – 2) – g – α.
Es ist somit das Geschlecht einer Raumkurve dem Geschlechte ihrer ebenen Projektion und jenem eines ebenen Schnittes ihrer abwickelbaren Fläche gleich.
Durch jeden Punkt des Raumes gehen an eine Raumkurve y doppelt berührende Ebenen; die Gesamtheit dieser Ebenen umhüllt eine der Raumkurve doppelt umschriebene abwickelbare Fläche. In jeder Ebene gibt es x Punkte, in denen sich zwei Erzeugende einer abwickelbaren Fläche schneiden. Die Gesamtheit aller dieser Punkte gehört einer Kurve an, die eine Doppelkurve der abwickelbaren Fläche darstellt. Nach dieser Doppelkurve durchschneidet sich die Fläche selbst. Die Klasse der doppelt umschriebenen abwickelbaren Fläche [2] ist 1/2 [r (r – 1) – n – 3 m], die Ordnung der Doppelkurve 1/2 [r (r – 1) – m – 3 n].
Das Bewegungsgesetz für eine Ebene kann gegeben sein durch die Bedingung, daß die Ebene in allen ihren Lagen a) Schmiegungsebene längs den Punkten einer Raumkurve sein soll, b) zwei gegebene Leitkurven oder Leitflächen berühren, c) eine Leitkurve und eine Leitfläche berühren, d) eine Leitkurve doppelt berühren, d.h. ihr doppelt umschrieben sein soll. – Unter allen abwickelbaren Flächen mit gegebener Rückkehrkurve ist geometrisch interessant und technisch wichtig die abwickelbare Schraubenfläche; bei ihr ist die Rückkehrkante eine Schraubenlinie; die Erzeugenden der Fläche sind gebildet durch die sämtlichen Tangenten der Schraubenlinie (s. Schraubenflächen). Unter den möglichen Flächen im Falle b) sollen nur die folgenden genannt werden: α) Die beiden Leitkurven sind Kreise oder Kegelschnitte und liegen in parallelen Ebenen; in beiden Fällen entstehen als abwickelbare Fläche zwei Kegelflächen zweiten Grades, deren Mittelpunkte auf der Verbindungslinie der Mittelpunkte der gegebenen Leitkurven liegen- und diese Linie im Verhältnis der Längen von zwei parallelen Halbmessern der genannten Kurven teilen, ß) Die beiden Leitkurven sind Kreise bezw. Kegelschnitte, in zwei unter einem beliebigen Winkel zueinander geneigten Ebenen; die abwickelbare Fläche ist eine Fläche von der achten Ordnung und vierten Klasse und besitzt die gegebenen Kegelschnitte als Doppellinien und überdies zwei weitere Kegelschnitte als Doppelkurven. Liegt einer der beiden Leitkegelschnitte in unendlicher Ferne und ist ersetzt durch einen senkrechten Kreiskegel als Richtungskegel, so ist die abwickelbare Fläche eine Böschungsfläche; ihre Tangentialebenen besitzen sämtlich gegen eine zur Achse des Leitkegels senkrechte Ebene die nämliche Neigung, γ) Die beiden Leitflächen sind Flächen zweiten Grades; die denselben umschriebene abwickelbare Fläche ist eine Fläche von der achten Ordnung und der vierten Klasse, sie besitzt vier Kegelschnitte als Doppelkurven und geht in zwei Kegelflächen zweiten Grades über für den Fall, daß die Leitflächen Kugeln werden. Ist eine der gegebenen Leitflächen leuchtend, die andre beleuchtet, so bilden die Berührungskurven ihrer gemeinsam umschriebenen abwickelbaren Fläche die Grenze des Halb- bezw. Kernschattens (s. Flächen zweiten Grades, S. 66). Der Fall c) ist von Wichtigkeit, wenn die Leitkurve ein Kegelschnitt ist, und zwar eine in unendlicher Ferne liegende Kreislinie, die durch einen senkrechten Kreiskegel ersetzt ist. Die entstehende abwickelbare Fläche ist dann wieder eine Böschungsfläche. Wird die Fläche in der Richtung der Achse des Kegels durch parallele Lichtstrahlen beleuchtet, so stellt die genannte Böschungsfläche eine Fläche gleicher Beleuchtungsstärke dar, und ihre Berührungslinie mit der Fläche ist eine Linie gleicher Beleuchtungsstärke, das ist eine Isophote (s. Schattenkonstruktionen). Im Falle d) gibt es außer der Tangentenfläche der Raumkurve im allgemeinen stets noch eine weitere abwickelbare Fläche, deren Erzeugende die Kurve doppelt berühren; eine Ausnahme hiervon macht nur die Raumkurve dritter Ordnung, die außer ihrer Tangentenfläche eine weitere, ihr doppelt umschriebene abwickelbare Fläche nicht besitzt; s.a. Zylinder und Kegelflächen. – Beleuchtung der abwickelbaren Flächen. Wird eine abwickelbare Fläche durch parallele Lichtstrahlen beleuchtet, so ergibt sich ihr zugehöriges Isophotensystem mittels des Richtungskegels; die Isophoten für eine abwickelbare Fläche sind Mantellinien oder Erzeugende der Fläche und parallel zu den entsprechenden Isophoten des Richtungskegels. S.a. Kegelflächen, Böschung- und Schraubenflächen [3], [4] und [5].
Erzeugung einer windschiefen Fläche. Das Bewegungsgesetz der Geraden kann dadurch gegeben sein, daß die bewegte Gerade entweder drei gegebene Kurven, die Leitlinien, in jeder ihrer Lagen treffen, oder aber, daß sie drei gegebene Flächen, die Leitflächen, stets berühren soll. Sind die Leitlinien oder Leitflächen algebraisch, so ist auch die windschiefe Fläche eine algebraische Fläche von bestimmter Ordnung und Klasse, und zwar sind Ordnung und Klasse stets einander gleich, weshalb man von windschiefen Flächen bestimmten Grades sprechen kann. Der Grad n einer windschiefen Fläche läßt sich aus den Ordnungszahlen n1 n2 und n3 ihrer Leitlinien A1, A2 und A3 ausdrücken, und zwar erhält man n = 2 · n1 · n2 · n3. Diese Gradzahl vermindert sich, sobald die Leitlinien gemeinsame Punkte besitzen, und zwar wird, wenn s3, s2 und s1 die Zahl der gemeinsamen Punkte zwischen den Leitlinien A1 A2 und A3 bezeichnen, n = 2 · n1 · n2 · n3 – n1 s1 – n2 s2 – n3 s3. Es ist klar, daß die Leitlinien A1, A2, A3 vielfache Kurven der windschiefen Fläche darstellen, und zwar beträgt der Grad der Vielfachheit n2 · n3, n1 · n3 und n1 · n2 bezw. und verringert sich um die Beträge n2 n3 – s, n1 n3 – s2 und n1 · n2 – s3 beim Vorhandensein von s1, s2 und s3 gemeinsamen Punkten zwischen den gegebenen Leitlinien. Die Leitlinien können aus geraden oder krummen Linien bestehen. Folgende vier Hauptgruppen von windschiefen Flächen sind denkbar: 1. die drei Leitlinien sind gerade, man erhält die windschiefen [64] Flächen zweiten Grades; 2. zwei Leitlinien sind gerade, eine Leitlinie ist krumm; 3. eine Leitlinie ist gerade, zwei sind krumm; 4. alle drei Leitlinien sind krumm. In allen vier Fällen kann überdies eine der Leitlinien in unendlicher Ferne liegen. Liegt eine gerade Leitlinie in unendlicher Ferne, so ist sie ersetzt durch eine Ebene, zu der die Erzeugenden der Fläche parallel laufen; man erhält eine windschiefe Fläche mit einer Leit- oder Richtungsebene. Ist dagegen eine krumme Leitlinie im Unendlichen vorausgesetzt, so ist sie ersetzt durch einen Kegel, zu dessen Mantellinien die Erzeugenden der windschiefen Fläche parallel laufen müssen, und man erhält eine windschiefe Fläche mit einem Leit- oder Richtungskegel.
Tangentialebene einer windschiefen Fläche. Jede durch eine Erzeugende B einer windschiefen Fläche gelegte Ebene E ist eine Tangentialebene der windschiefen Fläche; ihr Berührungspunkt mit der Fläche ist der Schnittpunkt b der Verbindungslinie c d der Schnittpunkte c und d der Nachbarerzeugenden C und D von B mit der Ebene E. Diese Verbindungslinie ist zugleich Tangente an die Schnittkurve der Tangentialebene E mit der windschiefen Fläche. Die Erzeugende B und die Tangente cd bilden die beiden Haupttangenten der windschiefen Fläche im Punkte b. Die Gesamtheit aller durch eine Erzeugende B gehenden Tangentialebenen der windschiefen Fläche bildet ein Ebenenbüschel projektiv zu der Punktreihe ihrer Berührungspunkte längs der Erzeugenden. Die sämtlichen zweiten Haupttangenten längs den Punkten einer Erzeugenden einer windschiefen Fläche liegen auf einem windschiefen Hyperboloide, das sich längs der Erzeugenden an die windschiefe Fläche anschmiegt. Im übrigen gibt es längs einer Erzeugenden einer windschiefen Fläche unzählig viele die windschiefe Fläche berührende windschiefe Hyperboloide bezw. windschiefe Paraboloide. Zu jeder Tangentialebene längs den Punkten einer windschiefen Fläche geht durch ihren Berührungspunkt mit der Fläche eine Normale zu letzterer, und diese Normalen bilden ein windschiefes Paraboloid, das zur Erzeugenden gehörige Normalenparaboloid. Eine Tangentialebene einer windschiefen Fläche schneidet aus letzterer im allgemeinen eine Kurve nter Ordnung heraus, die in die gerade Erzeugende und in eine Kurve von der Ordnung n – 1 zerfällt. Letztere trifft die Erzeugende einerseits in dem Berührungspunkt der Tangentialebene mit der Fläche und außerdem in n – 2 Punkten, in denen die Erzeugende noch von andern Erzeugenden der Fläche getroffen wird, welche Punkte also einer Doppellinie der Fläche angehören. In den Punkten dieser Doppellinie besitzt die windschiefe Fläche zwei voneinander verschiedene Tangentialebenen, die aber unter besonderen Umständen zusammenfallen können. Solche Punkte, in denen dies stattfindet, heißen Kuspidalpunkte der Fläche. Es kann endlich bei der Bewegung einer Geraden auch vorkommen, daß dieselbe zwei- oder mehreremal dieselbe Lage im Raum einnimmt; eine solche Erzeugende ist dann eine Doppel- oder mehrfache Erzeugende der windschiefen Fläche. Liegt der Berührungspunkt einer Tangentialebene mit einer windschiefen Fläche in unendlicher Ferne, so heißt die Ebene eine asymptotische Ebene der Fläche; eine durch die Erzeugende senkrecht zur asymptotischen Ebene geführte Tangentialebene hat als Berührungspunkt jenen Punkt, der der Nachbarerzeugenden am nächsten liegt; er heißt der Mittel- oder Zentralpunkt der Erzeugenden. Die sämtlichen Mittelpunkte der Erzeugenden liegen auf der Striktionslinie der windschiefen Fläche.
Ebener Schnitt einer windschiefen Fläche. Eine beliebige Ebene durchschneidet eine windschiefe Fläche n ten Grades nach einer Linie nter Ordnung, die eine Anzahl Doppel- oder vielfacher Punkte enthalten kann, je nachdem die Schnittebene die auf der windschiefen Fläche vorhandenen Doppel- oder mehrfachen Erzeugenden trifft. Enthält die Schnittebene eine Erzeugende, ist also eine Tangentialebene der windschiefen Fläche, so zerfällt der ebene Schnitt in eine Gerade und eine Linie n – 1ter Ordnung. Geht die Schnittebene durch zwei nicht benachbarte Erzeugende hindurch, so besteht die Schnittkurve aus zwei Geraden und aus einer Linie von der n – 2ten Ordnung.
Tangentenkegel an einer windschiefen Fläche. Soll von einem nicht auf der Oberfläche einer windschiefen Fläche liegenden Punkte ein Tangentenkegel an die Fläche gelegt werden, so führt man durch den Punkt und jede Erzeugende je eine Ebene und bestimmt deren Berührungspunkt mit der Fläche. Die Verbindungslinie dieser Berührungspunkte ist die Berührungslinie des Tangentenkegels; sie stellt, im Falle die Spitze des Tangentenkegels eine Lichtquelle ist, die Selbstschattengrenze der windschiefen Fläche dar. Der Schlagschatten der windschiefen Fläche auf eine bestimmte Ebene ist dann durch den Durchschnitt des Tangentenkegels mit der genannten Ebene festgelegt. Die windschiefen Flächen finden mannigfache Anwendung in der Technik, so als Fugenflächen bei Steinkonstruktionen, wie z.B. beim schiefen Tonnengewölbe (s. Gewölbe), ferner als Laibungsflächen für Gewölbe (windschiefe Wölbfläche), dann als Schraubenflächen im Maschinenbau.
Erzeugung einer Umhüllungsfläche. Eine solche Fläche entsteht durch Bewegung irgend einer Fläche nach einem bestimmten Gesetze, etwa derart, daß irgend ein in fester Verbindung mit der beweglichen Fläche befindlicher Punkt eine gegebene Leitlinie durchläuft. Hierbei kann die bewegliche Fläche ihre Gestalt unverändert beibehalten oder diese ebenfalls nach einem gegebenen Gesetze ändern. In beiden Fällen schneiden sich je zwei aufeinander folgende Lagen der beweglichen Fläche nach einer Linie, der Charakteristik der Umhüllungsfläche. Ist z.B. die bewegliche Fläche eine Kugel, so bestehen die Charakteristiken aus Kreisen, deren Ebenen senkrecht stehen auf der jeweiligen Bewegungsrichtung. So ist z.B. in Fig. 2 eine Umhüllungsfläche dargestellt, die zugleich eine Umdrehungsfläche ist. Ihre Leitlinie ist eine Kreislinie, die Charakteristiken sind gleichfalls Kreislinien und stehen senkrecht zur Leitlinie. Ist die Leitlinie eine Schraubenlinie und die bewegliche Fläche eine Kugel, deren Mittelpunkt auf der Schraubenlinie fortrückt, so entsteht als Umhüllungsfläche die schraubenförmige Röhrenfläche, s. Schraubenflächen. Auch der senkrechte Kreiszylinder bezw. Kreiskegel, desgleichen alle Umdrehungsflächen sind gleichzeitig Umhüllungsflächen von Kugeln, bei denen der Mittelpunkt auf der Achse der Umdrehungsfläche[65] sich bewegt, während der Halbmesser entweder unverändert bleibt oder sich nach einem bestimmten, durch die Meridianlinie ausgedrückten Gesetze verändert. Tangentialebene, Tangentenkegel bezw. -zylinder, desgleichen ebene Schnitte können mit Zuhilfenahme der beweglichen Fläche und der zugehörigen Charakteristiken konstruktiv ermittelt werden. Vgl. a. die besonderen Artikel: Flächentheorie, Flächen zweiten Grades, Ebene, Enveloppen, Fußpunktflächen, Kegelflächen, Konoidflächen, Schraubenflächen, Zylinderflächen, Cylindroid u.s.w. in analytischer Behandlung.
Literatur: [1] Fiedler, Die darstellende Geometrie der krummen Linien und Flächen,. Leipzig 1885. – [2] Peschka, Darstellende und projektive Geometrie, Bd. 2, Wien 1884. – [3] Wiener, Lehrbuch der darstellenden Geometrie, Bd. 2, Leipzig 1887. – [4] De la Gournerie, Traité de géométrie descriptive, Paris 1880, Bd. 2. – [5] Gugler, Lehrbuch der deskriptiven Geometrie, Stuttgart 1874. – [6] Rohn und Papperitz, Darst. Geometrie, 1893–96.
Vonderlinn.
Buchempfehlung
Wilbrandt, Adolf von
Gracchus der Volkstribun. Trauerspiel in fünf Aufzügen
Die Geschichte des Gaius Sempronius Gracchus, der 123 v. Chr. Volkstribun wurde.
62 Seiten, 4.80 Euro
Im Buch blättern
Ansehen bei Amazon
Buchempfehlung
Romantische Geschichten II. Zehn Erzählungen
Romantik! Das ist auch – aber eben nicht nur – eine Epoche. Wenn wir heute etwas romantisch finden oder nennen, schwingt darin die Sehnsucht und die Leidenschaft der jungen Autoren, die seit dem Ausklang des 18. Jahrhundert ihre Gefühlswelt gegen die von der Aufklärung geforderte Vernunft verteidigt haben. So sind vor 200 Jahren wundervolle Erzählungen entstanden. Sie handeln von der Suche nach einer verlorengegangenen Welt des Wunderbaren, sind melancholisch oder mythisch oder märchenhaft, jedenfalls aber romantisch - damals wie heute. Michael Holzinger hat für den zweiten Band eine weitere Sammlung von zehn romantischen Meistererzählungen zusammengestellt.
- Novalis Die Lehrlinge zu Sais
- Adelbert von Chamisso Adelberts Fabel
- Jean Paul Des Feldpredigers Schmelzle Reise nach Flätz
- Clemens Brentano Aus der Chronika eines fahrenden Schülers
- Friedrich de la Motte Fouqué Eine Geschichte vom Galgenmännlein
- E. T. A. Hoffmann Der goldne Topf
- Joseph von Eichendorff Das Marmorbild
- Ludwig Achim von Arnim Die Majoratsherren
- Ludwig Tieck Die Gemälde
- Wilhelm Hauff Die Bettlerin vom Pont des Arts
428 Seiten, 16.80 Euro
Ansehen bei Amazon
- ZenoServer 4.030.014
- Nutzungsbedingungen
- Datenschutzerklärung
- Impressum