Online-Bibliothek

Pendel

[560] Pendel (lat. Pendulum, »das Hangende«), in seiner einfachsten Form ein an einem Faden aufgehängter schwerer Körper.

Fig. 1. Pendel.

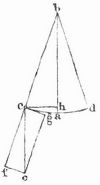
Denkt man sich den Faden gewichtslos und den Körper als ein einziges schweres Massenteilchen, so hat man ein einfaches oder mathematisches P. Entfernt man das P. aus seiner lotrechten Gleichgewichtslage ab (Fig. 1) und überläßt es dann sich selbst, so kehrt es unter der Einwirkung der Schwerkraft mit beschleunigter Geschwindigkeit dahin zurück, indem es einen Kreisbogen ca beschreibt; in der Gleichgewichtslage angelangt, kann es aber nicht plötzlich zur Ruhe kommen, sondern es geht nach dem Gesetz der Trägheit vermöge der erlangten Geschwindigkeit jenseits über jene hinaus, indem es mit abnehmender Geschwindigkeit einen ebenso großen [560] Bogen ad durchläuft, an dessen Ende d seine Geschwindigkeit durch die entgegenwirkende Schwerkraft erschöpft ist. Die Bewegung des Pendels von c bis d heißt eine halbe, die Bewegung bis zur Rückkehr nach c eine ganze Schwingung, der Winkel abc, den der Faden in seiner äußersten Lage mit der Gleichgewichtslage bildet, die Schwingungsweite (Amplitüde). In einer zweiten Schwingung kehrt das P. wieder von d in seine anfängliche Lage c zurück und würde so in unaufhörlicher Wiederholung derselben Bewegung mit gleichbleibender Amplitüde fortschwingen, wenn nicht äußere Hindernisse, nämlich die Reibung am Aufhängepunkt und der Widerstand der Luft, die Amplitüde immer kleiner machten und das P. endlich in der Gleichgewichtslage zur Ruhe brächten. Die Kraft, die das P. in die Gleichgewichtslage zurückzukehren nötigt, ist nicht die ganze Schwerkraft, sondern nur ein Teil (eine Komponente) derselben. Stellt nämlich in der Figur ce die vertikal abwärts wirkende Schwerkraft vor, so kann man sich dieselbe nach dem Parallelogramm der Kräfte in zwei Seitenkräfte cf und cg zerlegt denken, von denen erstere in die Richtung des Fadens, letztere in die Richtung der Berührungslinie des Kreisbogens, also in die Richtung der Bewegung fällt, die der Pendelkörper in Punkt c besitzt; nur diese letztere kann die Ursache der Bewegung sein, während jene keinen weitern Erfolg hat, als den Faden gespannt zu erhalten. Zieht man nun ch senkrecht zu ab, so folgt aus der Ähnlichkeit der Dreiecke ceg und cbh, daß sich die bewegende Kraft cg zur ganzen Schwerkraft verhält wie die Entfernung ch zur Pendellänge bc, oder daß die bewegende Kraft der Entfernung des Pendelkörpers von der Gleichgewichtslage des Fadens proportional ist. Wenn die Amplitüden nur klein sind, d.h. 2–3° nicht überschreiten, so ist der bogenförmige Weg ca, den der Pendelkörper bis zu seiner Gleichgewichtslage zurückzulegen hat, von der geradlinigen Strecke ch nicht merklich verschieden; da nun die treibenden Kräfte in demselben Verhältnis stehen wie die zu durchlaufenden Wege, so leuchtet ein, daß das P. bis zur Gleichgewichtslage dieselbe Zeit braucht, gleichviel ob seine Amplitüde 3 oder 2° oder nur wenige Bogenminuten oder -Sekunden beträgt. Bei kleinen Amplitüden sind also alle Schwingungen des Pendels von gleicher Dauer (isochron). Dieses Gesetz des Isochronismus der Pendelschwingungen wurde von Galilei entdeckt. Bei kleinen Schwingungen ist demnach die Schwingungsdauer unabhängig von der Amplitüde; sie wird (an ein und demselben Ort) nur durch die Länge des Pendels bedingt, und zwar verhalten sich die Schwingungszeiten ungleich langer P. wie die Quadratwurzeln aus den Pendellängen, d.h. die Schwingungszeiten verhalten sich wie 1,2,3..., wenn sich die Pendellängen wie 1,4,9... verhalten. Das mathematische P. besteht nur in der Idee; jedes wirklich ausgeführte P. ist ein physisches, materielles oder zusammengesetztes P. Es besteht gewöhnlich aus einer Stange, die an einer Schneide oder an einer dünnen. biegsamen Stahlfeder aufgehängt ist und nahe ihrem untern Ende als schweren Körper eine flache Linse trägt. Da jedes Massenteilchen des physischen Pendels um so schneller zu schwingen bestrebt ist, je näher es dem Aufhängungspunkt liegt, und da doch alle Teilchen durch ihren festen Zusammenhang gezwungen sind, gleichzeitig zu schwingen, so werden die dem Aufhängungspunkt näher gelegenen Teilchen in ihrer Bewegung verzögert, die entfernter gelegenen aber beschleunigt. Ein dazwischenliegender Punkt, dessen Bewegung weder verzögert noch beschleunigt wird, der vielmehr genau so schwingt, wie es sein Abstand vom Aufhängungspunkt fordert, heißt der Schwingungsmittelpunkt, und sein Abstand vom Aufhängungspunkte, die reduzierte Pendellänge; diese gibt die Länge desjenigen mathematischen Pendels an, das dieselbe Schwingungsdauer hat wie das gegebene physische. Für das physische P. gelten, wenn man unter seiner Länge die reduzierte Pendellänge versteht, dieselben Schwingungsgesetze wie für das mathematische. Vertauscht man bei einem physischen P. den Schwingungsmittelpunkt mit dem Aufhängungspunkt, so schwingt es in beiden Lagen gleich schnell. Mit Hilfe dieses Satzes läßt sich die reduzierte Pendellänge leicht bestimmen; man bedient sich hierzu des Reversionspendels (Differentialpendel), an dessen Stange sich außer der gewöhnlichen Aufhängungsachse noch eine zweite verschiebbare befindet; letztere wird durch Probieren in die Lage gebracht, daß das P. an ihr hängend genau soviel Zeit zu einer Schwingung braucht wie vorher, als es an der ersten Aufhängungsachse hing. Die reduzierte Pendellänge ist dann gleich dem Abstande der beiden Aufhängungsschneiden. Um die Messungen zu variieren, werden P. von verschiedenem Gewicht und verschiedener Länge benutzt. Schon Huygens hatte vorgeschlagen, die Länge des Sekundenpendels, d.h. eines Pendels, das in einer Sekunde eine (halbe) Schwingung vollendet, als Einheit des Längenmaßes zu wählen. In England wurde dieser Vorschlag insofern zur Ausführung gebracht, als man das Verhältnis des Yards zur Länge des Londoner Sekundenpendels gesetzlich feststellte. Die zur Zeit der französischen Revolution zur Einführung eines neuen Maßsystems niedergesetzte Kommission verwarf jedoch diese Idee, weil eine solche Einheit ein fremdes Element, die Zeit, enthalte.

Die Schwingungsdauer t eines Pendels wird ausgedrückt durch die Formel t = 2π√(l/g) oder = π√(l/g), je nachdem man darunter die Dauer einer ganzen oder halben Schwingung versteht (Pendelgesetz), l bedeutet die (reduzierte) Pendellänge, g die Beschleunigung der Schwere (Akzeleration), d.h. die Geschwindigkeit eines frei fallenden Körpers am Ende der ersten Fallsekunde, und, π die Zahl 3,14159, d.h. das Verhältnis des Umfanges eines Kreises zu seinem Durchmesser. Die Beschleunigung der Schwere, die als Maß für die Anziehungskraft der Erde anzusehen ist, läßt sich aus dem freien Fall selbst, weil diese Bewegung zu rasch ist, nicht mit Sicherheit ermitteln; ist aber l gemessen und t beobachtet, so kann man g mit großer Genauigkeit aus obiger Formel berechnen. So beträgt z. B. in Berlin die Länge des Sekundenpendels 994,24 mm, und daraus ergibt sich für Berlin g = 981,273 cm. Solche absolute Messungen werden aber nur an wenigen Orten ausgeführt, wie in neuerer Zeit in Potsdam durch Helmert. Zu den zahlreichen Bestimmungen der Schwerkraft (relative Schwermessungen) an der Erdoberfläche dienen die sogen. invariabeln P. Diese besitzen jetzt meist eine Schwingungsdauer von nahezu ¹/₂ Sekunde und haben durch v. Sterneck eine große Verbreitung erlangt. Betrachtet man in der obigen Formel l als konstant, so ergibt sich, daß für ein invariables P. an allen Orten das Produkt g.t eine Konstante ist. Wird diese Konstante für einen Ausgangsort, für den g bekannt ist, bestimmt, so kann g an beliebig vielen[561] Orten durch Beobachtung der Schwingungsdauer des invariabeln Pendels berechnet werden. Es werden hiernach Unterschiede in der Größe der Schwerkraft gemessen. Die Unveränderlichkeit des Pendels wird nach der Rückkehr von dem Ausgangsort durch wiederholte Beobachtung seiner Schwingungsdauer nachgewiesen. Bei der Bestimmung der letztern ist auch das durch das schwingende P. verursachte Mitschwingen seines Stativs, die Temperatur, der Luftdruck und, in geringerm Maß, auch die Luftfeuchtigkeit in Rechnung zu ziehen. Entsprechend der Änderung der Schwerkraft mit der geographischen Breite, der Meereshöhe und der am Beobachtungsort lagernden Erdmassen ist die Länge des Sekundenpendels verschieden für verschiedene Orte der Erdoberfläche, und zwar nimmt sie mit der Meereshöhe ab und von dem Äquator nach den Polen hin zu (s. Schwere). Auch die Dichte (das spezifische Gewicht) des Erdkörpers wurde von Airy durch Pendelbeobachtungen bestimmt (s. Gravitation). Ein schwingendes P. hat vermöge der Trägheit das Bestreben, in seiner Schwingungsebene zu verharren, und hält dieselbe auch der Umdrehung der Erde gegenüber fest; darauf gründet sich der Foucaultsche Pendelversuch (s. d.), der die Umdrehung der Erde um ihre Achse auf direkte Weise anschaulich macht. Huygens benutzte das P. zuerst bei den Uhren, um die durch ein Gewicht oder eine Feder hervorgebrachte Bewegung des Räderwerkes nach gleichen Zeitintervallen immer auf einen Augenblick zu hemmen und dadurch den sonst eintretenden ungleichförmigen Gang in einen gleichmäßigen zu verwandeln.

Fig. 2. Kompensationspendel.

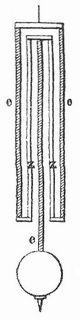
Da die Schwingungsdauer eines Pendels bei seiner Verlängerung sich vergrößert, so muß eine mit gewöhnlichem P. versehene Uhr bei hoher Temperatur zu langsam, bei niedriger Temperatur zu schnell gehen. Bei dem Rostpendel (Kompensationspendel, Fig. 2) wird diese den gleichmäßigen Gang der Uhr störende Einwirkung der Wärme ausgeglichen (»kompensiert«), indem die kürzern, aber stärker sich ausdehnenden Zinkstangen zz die Pendellinse ebensoweit nach oben schieben, als sie durch die längern, aber weniger ausdehnungsfähigen Eisenstangen eee nach abwärts geschoben wird. Neuerdings hat man übrigens im Nickelstahl ein Material gefunden, das sich mit der Temperatur nicht merklich ausdehnt, somit Kompensationspendel unnötig macht.

Gibt man dem schweren Körper eines einfachen Pendels, wenn es sich eben in seiner größten Ausweichung befindet, einen passend abgemessenen Stoß senkrecht zur Schwingungsebene, so beschreibt er von nun an mit gleichförmiger Geschwindigkeit eine Kreislinie um den Punkt der Gleichgewichtslage und wird jetzt konisches oder Zentrifugalpendel genannt. Die Zeit seines Umlaufs ist gleich der ganzen Schwingungsdauer des gewöhnlichen Pendels von gleicher Länge. Man kann die Zentrifugalpendel ebenfalls bei Uhren benutzen; da aber ihre Aufhängung Schwierigkeiten verursacht, so wendet man sie häufiger zur Regulierung der Umdrehung astronomischer Instrumente, bei Registrierapparaten und bei den Drehfeuern der Leuchttürme an. Beim Zykloidenpendel wird der Schwingungsmittelpunkt durch geeignete Führungen gezwungen, sich längs einer Zykloide zu bewegen. Für dieses ist die Schwingungsdauer vollkommen unabhängig von der Amplitüde. Ein Bifilarpendel ist eine horizontale, an zwei Fäden aufgehängte Stange. Dreht man sie aus ihrer Richtung, so daß die Fäden schräg laufen, so wird sie entsprechend gehoben und pendelt beim Loslassen zurück. Gleiches gilt für das Kontrafilar- oder Horizontalpendel (s. d.).

Bei dem Federpendel tritt an Stelle der Schwerkraft die elastische Kraft einer Feder. Die Dauer einer ganzen Schwingung beträgt 2π√(m/f), wobei m die schwingende Masse (Gewicht in kg dividiert durch 9,81, s. Masse) und f die Kraft in kg, welche die Elongation lm hervorbringen würde. Von der unverändert gleichen Dauer dieser elastischen Schwingungen macht man eine wichtige Anwendung zur Regulierung der Taschenuhren; indem sich nämlich die an der Unruh befestigte zarte Spiralfeder in gleichdauernden Pulsen abwechselnd auseinander- und wieder zusammenwindet, bewirkt sie, daß die Hemmung des Steigrades durch die Unruh in genau gleichen Zeitabschnitten erfolgt und der Sekundenzeiger demnach beim Fortrücken zu jedem seiner Sprünge genau die gleiche Zeit braucht. Statt einer Spiralfeder kann auch einfach ein elastischer Draht zur Herstellung eines solchen Torsionspendels benutzt werden, indem man eine horizontale Stange daran hängt, die bei Verdrillung zurückpendelt.

Der Einfluß der Temperatur auf den Radius und damit die Schwingungsdauer wird bei der Kompensationsunruhe nach ähnlichem Prinzip wie bei dem Rostpendel durch Anwendung einer Kombination von zwei Metallen beseitigt. Graphisches (schreibendes) P. ist ein P., das seine Schwingungen in Form einer Wellenlinie etwa mittels eines daran befestigten Pinsels auf einem darunter fortgezogenen Papierstreifen auszeichnet. Doppelpendel ist eine Kombination von zwei Pendeln verschiedener Schwingungsdauer und Schwingungsebene, von denen z. B. das eine an der Linse des andern angehängt ist. Wird dieses als schreibendes P. eingerichtet, so entstehen auf einem ruhenden Papier die sogen. Lissajousschen Figuren, s. Kombinationsfiguren. Gewöhnlich werden hierzu Federpendel, z. B. Stimmgabeln, verwendet. Magnetisches P. ist ein P., das statt durch die Schwerkraft durch magnetische oder elektrodynamische Kräfte beeinflußt wird. Ein Beispiel ist eine schwingende Magnetnadel. Anwendung findet es beim Magnetometer zur Bestimmung von Polstärken und Feldintensitäten, ferner bei Arons Elektrizitätszähler zur Messung des Stromverbrauchs bei elektrischen Anlagen. v. Waltenhofens Induktionspendel ist ein P. mit kupferner Linse, das, sobald ein magnetisches Feld erregt wird, durch die in dieser entstehenden Wirbelströme rasch zur Ruhe gebracht wird, also dazu dienen kann, das bei Galvanometern, Magnetometern etc. verwertete Prinzip der Kupferdämpfung sowie das der Wirbelstrombremse für Effektbestimmung von Motoren zu erläutern. Elektrische P. sind Elektroskope. Ballistisches P. heißt ein von Robins erfundener Apparat zur Messung der Anfangsgeschwindigkeit von Geschossen und damit der Kraft des Pulvers (vgl. Ballistik).