Online-Bibliothek

Triangulierung [1]

[610] Triangulierung (Triangulation, Dreiecksmessung, trigonometrische Punktbestimmung), geodätische Bestimmungsmethode. Sie bestimmt für ein System von Festpunkten (Dreieckspunkten, trigonometrischen Punkten oder Stationen), das im Gelände dauerhaft bezeichnet ist, die Orte auf der mathematischen Erdoberfläche in Koordinaten (s. Bd. 5, S. 620). Sie liefert bei umfangreichen Messungen die Grundlage, besonders bei der Gradmessung (s. Erde, Bd. 3, S. 482), der Landesvermessung (s. Bd. 6, S. 65) und der Katastervermessung (s. Bd. 5, S. 406).

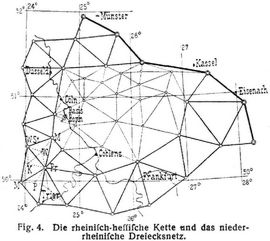
Der Grundgedanke dieser Bestimmungsmethode wurde von Snellius 1615 bei der Messung eines Meridianbogens zuerst zur Ausführung gebracht. Er ist der folgende: Es werden Punkte im Gelände derart ausgewählt, daß ihre Verbindungslinien ein System aneinander hängender Dreiecke bilden. Werden in diesen Dreiecken die Winkel und die Länge irgend einer Linie gemessen, so können sämtliche Dreiecke aufgelöst werden; ist weiterhin noch das Azimut irgend einer Linie in einem Koordinatensystem gegeben, so können die Koordinaten sämtlicher Dreieckspunkte und hieraus alle Punktabstände berechnet werden. Je nach Ausdehnung des Vermessungsgebiets sind die Koordinaten rechtwinklig-ebene, -sphärische bezw. -sphäroidische oder geodätisch-geographische (s. Bd. 5, S. 620). Ist die Aneinanderreihung der Dreiecke derart, daß sie in Gestalt einer Kette nach einer Richtung hin sich erstrecken oder ein Gebiet umrahmen, wie z.B. die stark gezeichneten Dreiecke der Fig. 4, so spricht man von einer Dreieckskette; bilden die Dreiecke in einem gegebenen Gebiet ein derart geschlossenes System, daß die Punkte gleichmäßig verteilt sind, so spricht man von einem Dreiecksnetz (vgl. das von der Kette in Fig. 4 umschlossene Netz), womit man auch ganz allgemein geschlossene Systeme verschiedener Anordnung bezeichnet, z.B. auch die der Fig. 5 und 6. Gleichbedeutend ist trigonometrisches Netz; dem entspricht die Bezeichnung trigonometrische Netzkarte oder Triangulierungskarte.

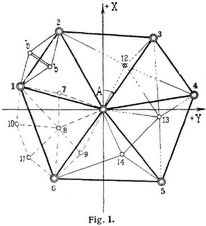
Die für die Zwecke der Landesvermessung über ein ganzes Staatsgebiet einheitlich durchgeführte Triangulierung heißt Landestriangulierung. Sie zerfällt in Haupt- und Kleintriangulierung; die erstere wieder in Triangulierung I. und II. Ordnung, die letztere in III., IV. bis zu V. Ordnung. In diesen stufenweise einander untergeordneten Systemen werden die Dreiecksseiten nach und nach von etwa 50 km und mehr bis zu einigen Kilometern und für die Katastervermessung bis zu 1 km, ja 0,5 km herabgeführt, wobei gleichzeitig stufenweise die Messungs- und Berechnungsmethoden eine entsprechende Modifikation erfahren, und der Uebergang von der sphäroidischen Vermessungsfläche (s. Bd. 3, S. 483) zur ebenen vollzogen wird. Einen Einblick in die verschiedenen Methoden der trigonometrischen Punktbestimmung gewährt in einfacher Weise das in Fig. 1 in starken Linien dargestellte schematische Beispiel, welches dem Netz einer selbständigen Kleintriangulierung entspricht, etwa für den Gesichtskreis des Punktes A. Die Dreieckspunkte 1 bis 6 sind im Gelände so ausgewählt (Erkundung, Rekognoszierung des Netzes), daß sie gleichmäßig im Umkreis um A verteilt und nach den eingezeichneten Linien gegenseitig sichtbar sind. Eine derartige Anordnung bezeichnet man[610] als Zentralsystem. Die Punkte werden mit dauerhaften Marken bezeichnet (Vermarkung, Festlegung) und durch Signale gegenseitig sichtbar gemacht (Signalisierung). Auf allen Punkten A und 1 bis 6 werden alle Winkel der Figur oder alle von den einzelnen Punkten ausgehenden Richtungen mit dem Theodolit gemessen (Winkel- bezw. Richtungsmessung). Nun ist für irgend eine Seite des Netzes, z.B. 1–2, die Länge zu bestimmen. Da die unmittelbare Längenmessung für eine Dreieckseite selten ausführbar ist, wird eine passend gelegene, sicher zu messende Linie, die Basis (b b, Fig. 1), aufgesucht und gemessen. Hieraus wird wieder durch Anordnung einiger Dreiecke (Basisnetz) die gesuchte Linie, also 1–2, berechnet (vgl. Basismessung, Bd. 1, S. 561). Hierauf können, wenn zunächst vorausgesetzt wird, daß die Ausdehnung eine beschränkte ist und die Fehler der Messung außer acht gelassen werden sollen, alle Dreiecke aufgelöst werden. Wird nun weiterhin ein Punkt, z.B. A, als Anfangspunkt eines ebenen rechtwinkligen Koordinatensystems betrachtet und irgendeiner Linie, z.B. A–3, ein bestimmtes Azimut (Richtungs-, Neigungswinkel) beigelegt, so können mit Hilfe der Dreieckswinkel die Azimute der übrigen Linien berechnet werden, z.B. R_a.4 = R_a.3 + w_3.4 u.s.w. Ferner können mit Hilfe der berechneten Dreieckseiten s die Koordinaten y, x aller Punkte bestimmt werden, z.B. y₃ = s₃ sin R_a.3; x₃ = s₃ cos R_a.3 u.s.w.

Um auf Grund des bisher betrachteten einfachen Netzes weitere Punkte zu bestimmen (einzuschalten), können verschiedene Verfahren zur Anwendung kommen. So z.B. zeigt Fig. 1 eine Ausfüllung des Gebietes des Dreiecks A–1–6 mit einem diesem untergeordneten Dreiecksnetz der Punkte 7 bis 11, in der Figur mit gestrichelten Linien bezeichnet. Die im Gebiete des Polygons A–2–3–4–5–6 eingezeichneten Punkte 12, 13 und 14 zeigen die Punkteinschaltung durch Einschneiden, d.h. eine wiederholte Anwendung des einfachen und vereinten Vorwärts- und Rückwärtseinschneidens (s.d.).

A. Die trigonometrischen Feldarbeiten.

1. Erkundung des Netzes. Zur sachgemäßen Auswahl und gleichmäßigen Verteilung der Dreieckspunkte im Gelände derart, daß sowohl der geometrische Zusammenhang des Netzes gewahrt als auch die Bestimmung möglichst günstig und einfach wird, dient die Erkundung des Netzes. – Einige der wichtigsten Anforderungen sind: Gegenseitige Sichtbarkeit benachbarter Punkte; Möglichkeit des Anschlusses weiterer Messungen, exakter Vermarkung und Erhaltung des Punktes, sicherer Ausführung der Winkelmessung; Erzielung günstiger Bestimmungsfiguren bei möglichst geringem Arbeitsaufwand. – Zur gegenseitigen Sichtbarmachung sind häufig Ausholzungen und Durchhaue durch Wald oder Gebüsch notwendig. Für die Punkte der Haupttriangulierungen kommen besonders Erhöhungen, Berge, und im Flachlande auch Kirchtürme in Betracht. Bei der Kleintriangulierung ist die Möglichkeit eines guten Anschlusses der Kleinmessungen (Polygonisierung und Stückvermessung) von besonderer Bedeutung. – In einfachen Ketten und Netzen sind sehr spitze Winkel zu vermeiden. Das gleichseitige Dreieck ist im allgemeinen die zu erstrebende günstigste Figur (vgl. z.B. Fig. 4); bei der Einzelpunktbestimmung durch Einschneiden soll der Neupunkt möglichst im Schwerpunkt des nächst übergeordneten Systems liegen, so daß die bestimmenden Richtungen gleichlang und gleichmäßig im Umkreis verteilt sind (z.B. Fig. 1, Punkt 12, 13, 14). – Die Erkundung beginnt auf den gegebenen Anschlußpunkten, wobei auf jedem besuchten Punkte alle in Frage kommenden Sichten in Handskizzen verzeichnet werden. Bei der Erkundung für Haupttriangulierungen wird hierbei das ganze Netz vorläufig beobachtet und berechnet. Für solche Richtungen, welche durch Durchhaue freigelegt werden müssen, sind besondere, auf diese Rechnung gestützte Absteckungen erforderlich. In schwierigen Fällen kann außerdem der Bau hoher Umschaugerüste notwendig werden. – Das Projekt, welches bei der Erkundung unter sachgemäßer Auswahl und Ausscheidung der Sichten nach und nach entsteht, wird in der trigonometrischen Netzkarte dargestellt. Sie dient als Unterlage für die Beobachtung und Rechnung. Die allgemeine Anordnung der trigonometrischen Vorarbeiten ist kurz dargestellt in [24], wertvolle Winke und Erfahrungen geben [25], [26], vgl. a. [1], Bd. 3, und [2].

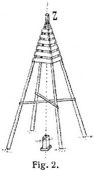
2. Vermarkung und Signalisierung. Die Dreieckspunkte werden im Gelände in der Regel durch Steinpfeiler mit eingemeißelter Marke, einem Kreuz oder Loch, bezeichnet. Zur weiteren Sicherung wird eine unterirdische Vermarkung hinzugenommen. So wird bei der preußischen Landesaufnahme unter der Steinsäule eine Platte so versenkt, daß ihre Kreuzmarke lotrecht unter derjenigen des Steinpfeilers liegt [10], vgl. Fig. 2. Bei der preußischen Katastervermessung werden die Punkte der Kleintriangulierung im freien Felde durch ein versenktes Drainrohr vermarkt, dessen Stellung durch seitwärts versenkte engere Rohre (exzentrische Vermarkung) gesichert wird [5]. – Vgl. a. [1], Bd. 2, Kap. 8. – Zudem werden alle Dreieckspunkte bei der Spezialvermessung aufgenommen und gegen benachbarte Grenzen oder andre feste Linien und Punkte eingemessen. Die Vermarkung der Dreieckspunkte der Landesvermessungen steht unter gesetzlichem Schutz. Außerdem wird eine Schutzfläche von einigen Quadratmetern um den Punkt für den Staat erworben, wenn nötig durch Enteignung. Bei denjenigen Dreieckspunkten, welche durch Kirchtürme bezeichnet werden, bildet die Mittellinie der Turmspitze (Helmstange) unter dem Knopf oder der Kreuzblume den Punkt. (In Photographien oder Skizzen darzustellen.) Daneben kommen bei wichtigen Punkten noch besondere Marken (Festlegungsbolzen, -schrauben) für Nebenpunkte, Instrumentstände u.s.w. hinzu.

Zur gegenseitigen Sichtbarmachung (Signalisierung) der Punkte genügen bei der Kleintriangulierung glatt behauene oder abgehobelte Stangen von etwa 5–6 m Länge und 1 dm Dicke. Sie werden etwa meterweise mit mattem, nicht glänzendem, schwarzweißem Anstrich und am[611] oberen Teile mit Zieltafeln (Fahnen u.s.w.) versehen. Im Boden werden sie über der Punktmarke durch angenagelte kräftige Streben befestigt und sorgfältig lotrecht gerichtet. Bei städtischen Kleintriangulierungen finden zuweilen weiße Zieltafeln mit schwarzen Zielstrichen Verwendung; auch eiserne Signale mit konischen Kappen u.s.w. sind hierfür geeignet. Für größere Entfernungen werden regelmäßige, vierseitige Pyramiden nach Fig. 2 von etwa 5 bis 8 m Höhe erforderlich. Die Dimensionen sind abhängig von der Zielweite. Der Zielpunkt ist die Mittellinie des Zapfens Z; diese soll in der Lotlinie über dem Vermarkungspunkte liegen. Ist das nicht der Fall, so ist eine Zentrierung erforderlich (s. weiter unten). – Bei dieser Art der Signalisierung wird der Theodolit unmittelbar auf dem zugehörigen Stativ aufgestellt; bei Haupttriangulierungen wird statt dessen in der Regel ein starker, etwa 1,25 bis 1,5 m hoher Holz- oder Steinpfeiler mit Instrumentplatte errichtet. – Kann die Beobachtung nicht vom Boden aus erfolgen, so ist ein erhöhter Beobachtungsstand erforderlich. Derartige Beobachtungspfeiler werden bis zu 25 m Höhe errichtet. Man unterscheidet je nach der Konstruktion Hängepfeiler und Standpfeiler. Die wichtigste Anforderung ist, daß der Pfeiler einen durchaus festen Instrumentstand bietet. Dazu ist ein solches Signal aus zwei ineinander gesetzten, vollständig getrennten Bauwerken aus starken Balken herzustellen, dem eigentlichen Instrumentpfeiler (Mittelpfeiler) und dem Stand mit den Treppen für Beobachter, Schreiber u.s.w. (Signalgerüst). Derartige Gerüste kosten bis zu 1500 ℳ. Weiteres hierüber s. [26]. Bei den Haupttriangulierungen werden fast ausschließlich erhöhte Beobachtungsstände aus Stein oder Holz von einigen Metern bis zu 25 m Höhe verwendet. Besondere Einrichtungen der Beobachtungsstände sind bei der Benutzung von Kirchtürmen erforderlich. Mitteilungen über den Signalbau und die Einrichtung der Beobachtungsstände (bei der preußischen Landestriangulation durch besondere Vorschriften geregelt) finden sich in [24]–[26] und [1], Bd. 3. Vgl. a. [27]. Die spezielle Anordnung der Vermarkung und Signalisierung bei den verschiedenen Landesvermessungen ist gegeben in den betreffenden Veröffentlichungen, z.B. [10]–[15]. Ueber die Verwendung besonderer Signale, wie Signalkugeln, -lampen u.s.w. s. Heliotrop (Bd. 5, S. 35).

3. Winkel- und Richtungsmessung. Die Bestimmung des von einem Dreieckspunkte ausgehenden Richtungssystems, z.B. für den Punkt A in Fig. 1, kann entweder geschehen durch Richtungsmessung (vgl. Bd. 7, S. 425) oder durch Winkelmessung.

a) Satzweise Richtungsmessung. 1. Vollständige Sätze. Bei fest aufgestelltem Theodolit, z.B. auf A, Fig. 1, werden die Zielpunkte 1, 2, ... 6 der Reihe nach eingestellt, und dabei werden die Kreisablesungen gemacht. Die einmalige Messung einer solchen Reihe 1, 2, 3 ... 6, (1) in rechtsläufiger Folge mit Prüfung der unveränderten Stellung des Instrumentes durch die Schlußablesung (1) nennt man einen einfachen Richtungssatz (Satz, Gyrus). Die zur Tilgung der Fehler der Instrumentachsen und der Stativstellung erforderliche Wiederholung in rückläufigem Sinn 1, 6, 5 ... 2, (1) bildet den zweiten Halbsatz, und das Mittel aus beiden Halbsätzen (Hin- und Rückgang) den vollständigen Satz. – Zur Erhöhung der Genauigkeit (Herabminderung, der Kreisteilungs-, Ablesungs-, Einstellungsfehler u.s.w.) ist eine mehrfache Wiederholung dieser Satzbeobachtungen erforderlich, wobei die einzelnen Sätze derart anzuordnen sind, daß alle Ablesungen für eine Richtung gleichmäßig über den Kreis verteilt werden. Dies geschieht dadurch, daß bei zwei diametralen Zeigern (Nonien oder Mikroskopen) der Kreis von Satz zu Satz derart verstellt wird, daß bei n Sätzen die Kreislagen um 180° : n voneinander abstehen. Die Anzahl der Sätze richtet sich nach der zu erzielenden Genauigkeit und der Leistung des Instruments. Um hierüber ein Urteil zu erlangen, muß der mittlere Fehler der Richtungsmessung aus den Beobachtungen abgeleitet werden nach der Formel

Hierin bedeuten m_r den mittleren Fehler einer in einem vollständigen Satz gemessenen Richtung, [v v] die Quadratsumme der aus den Abweichungen abgeleiteten zufälligen Fehler, v die Anzahl der Richtungen, n die Anzahl der Sätze. Der mittlere Fehler des aus n Sätzen gebildeten arithmetischen Mittels ist M_r = m_r : √n. – Vgl. [1], Bd. 1, Zahlenbeispiel in [49]. Für Kleintriangulierungen werden die Sätze je nach dem Instrument drei- bis sechsmal gemessen, bei Haupttriangulierungen acht- bis zwölfmal und mehr. Der mittlere Richtungsfehler für eine Satzbeobachtung liegt etwa zwischen den Grenzen ± 10'' und ± 1''. – Die satzweise Richtungsmessung mit sechs bis acht oder auch zehn Richtungen ist für Kleintriangulierungen im allgemeinen das günstigste, den geringsten Arbeitsaufwand erfordernde Messungsverfahren, und daher zu erstreben. – Aus den Ablesungen in den beiden Fernrohrlagen werden die Mittel gebildet. Danach werden die Sätze auf die erste Richtung als Anfangs- oder Nullrichtung bezogen durch Subtraktion der Mittel für die erste Richtung von den nachfolgenden Mitteln, und aus diesen so reduzierten Sätzen wird wieder das Mittel genommen. Zur Aufschreibung und Berechnung der Beobachtungen dienen besondere, gedruckte Formulare (Winkelbuch), welche bei den amtlichen Arbeiten vorgeschrieben sind. Weiteres hierüber sowie über die Anordnung der Rechnung in den amtlichen Anweisungen z.B. [5], vgl. a. [1], [3] und [4].

2. Unvollständige Sätze. Häufig treten jedoch Störungen dieser einfachen Anordnung ein, z.B. dadurch, daß Ziele unsichtbar werden oder nicht alle Ziele in einer Reihe vereinigt werden können. In diesen Fällen ist die Beobachtung so anzuordnen, daß aus derartigen unvollständigen Sätzen auf rechnerischem Wege (durch Ausgleichung) eine einheitliche Richtungsreihe abgeleitet werden kann. Hierbei ist zu beachten, daß jede Richtung eine entsprechende Genauigkeit erhält, daß die einzelnen Richtungssätze bei möglichst geringem Arbeitsaufwand einen möglichst innigen Zusammenhang haben, und daß der Einfluß der Kreisteilungsfehler durch zweckmäßige Anordnung der Kreistagen tunlichst vermindert wird. Ist auf einer Station eine große Anzahl von Richtungen zu beobachten, so ist es empfehlenswert, die Richtungen symmetrisch bei entsprechender Verteilung der Kreistagen zu gleichartigen Satzgruppen[612] zusammenzufassen, vgl. [28]. Die Ausgleichung unvollständiger Satzbeobachtungen (sogenannte Stationsausgleichung) erfolgt nach der Methode der kleinsten Quadrate (s.d.), vgl. hierüber [1]–[5], oder einem bei der englischen Landesvermessung angewendeten Näherungsverfahren, welches in [1], Bd. 1, § 59, [3] und [5] dargestellt ist. Das Näherungsverfahren besteht im wesentlichen darin, daß die Abweichungen gegen das arithmetische Mittel der unvollständigen Sätze gebildet, satzweise die mittleren Abweichungen (Satzverschiebung, Orientierung) berechnet und danach die einzelnen Sätze so verschoben werden, bis diese Verschiebungen nicht mehr größer sind als die Beobachtungsfehler. – Ueber besondere Verhältnisse der Richtungsmessung und deren Ausgleichung, namentlich für Haupttriangulierungen (zuerst von Struve und Bessel behandelt), Einführung der sogenannten Nullmarke u.s.w., s. [1], Bd. 1–3, sowie die Publikationen unter [10]–[16], [22]–[24] und [29].

b) Winkelmessung. Anstatt ein Richtungssystem r₁, r₂, r₃, ... r_n in eine einzige Beobachtungsreihe zusammenzufassen oder in einige mehrzahlige Reihen zu zerlegen, kann man auch das kleinste Richtungssystem, d.h. den Winkel, beobachten. Die Zerlegung eines mehrzahligen Richtungssystems in Winkel kann in verschiedener Weise geschehen. Werden die Richtungen eines Systems r₁, r₂, r₃, ... r_n in die Winkel r₁, r₂, r₁ · r₃, ... r₁ · r_n zerlegt, so hat man die sogenannte Einzelbeobachtung der Richtungen. An Stelle einer beliebigen, aus der Reihe der Ziele ausgewählten Anfangsrichtung kann auch eine besondere, dem System nicht angehörige Nullrichtung eingeführt werden, so daß die Winkel r₀ · r₁, r₀ · r₂, ... r₀ · r_n entstehen. Diese Nullrichtung, welche die Beziehung der Richtungen r₁ bis r_n vermittelt, ist so auszuwählen, daß ihre Einstellung möglichst günstig ist. Die einzelnen Winkel werden der erforderlichen Genauigkeit entsprechend mehrfach in verschiedenen Kreistagen gemessen (Anordnung wie bei der Richtungsmessung) oder bei Anwendung eines Repetitionstheodolits repetiert. Vgl. hierzu [3] und [5]. Wird das Richtungssystem r₁, r₂, r₃, ... r_n in die aufeinander folgenden Winkel r₁ · r₂, r₂ · r₃ ... r_n r₁ zerlegt, so füllen die Winkel zusammen den Horizont. Es tritt dann die Bedingung auf: Summe aller Winkel = 360°, und man hat für die Berechnung des Richtungssystems die Aufgabe einer Ausgleichung auf den Sollbetrag; es ist dies die einfachste Aufgabe der Stationsausgleichung. Die einzelnen Winkel sind auch hierbei mit entsprechender Anordnung der Kreistagen zu wiederholen oder durch Repetitionsmessung zu bestimmen. – Werden die Winkel so angeordnet, daß beliebige Kombinationen gebildet und überschüssige Bestimmungen erhalten werden, so ist das Richtungssystem nach der Methode der kleinsten Quadrate abzuleiten. Wegen solcher Stationsausgleichungen s. [1]–[5] sowie die in Bd. 6, S. 423 genannte Literatur. – Das günstigste Verfahren der Winkelmessung für Haupttriangulierung ist das von Schreiber in [29] entwickelte (Schreibersche Winkelmessung). Für das Richtungssystem r₁, r₂, r₃ ... r_n werden durch Bildung der Kombinationen ohne Wiederholung für je zwei Richtungen die ¹/₂ n(n – 1) Winkel gebildet, z.B. für n = 4 die 6 Winkel r₁ · r₂, r₁ · r₃, r₁ · r₄, r₂ · r₃, r₂ · r₄, r₃ · r₄. Diese Winkel werden, wenn das Gewicht der ausgeglichenen Richtungen = P (entsprechend P Richtungssätzen) sein soll, p = 2 P : n mal in beiden Fernrohrlagen in 180° : p voneinander abstehenden Kreistagen gemessen, wobei für die einzelnen Winkel die Kreisstellungen innerhalb des Intervalles 180° : p so zu bestimmen sind, daß die Richtungsablesungen symmetrisch über den Kreis verteilt werden. Dazu sind um 180° : p n, bezw. 180° : p (n – 1) voneinander abstehende Kreisstellungen erforderlich, je nachdem n eine ungerade oder gerade Zahl ist. Ein Schema für die Anordnung dieser Kreisstellungen s. in [29]. Durch dieses Verfahren wird bei der Ausführung von reinen Winkelmessungen unter möglichst großer Arbeitsersparnis bei Beobachtung und Rechnung erreicht: Das gegebene Beobachtungsgewicht für das Richtungssystem, die Gleichwertigkeit aller Richtungen, die Tilgung der systematischen Kreisteilungsfehler und außerdem die größte Freiheit für die Ausführung der Beobachtung, für die Ausnutzung günstiger Beleuchtung und für die Verteilung der Heliotropen. Diese Beobachtungsmethode ist bei der preußischen Landestriangulation für die Beobachtungen I. Ordnung vorgeschrieben. Weiteres s. [29], [1], Bd. 1, vgl. a. [49].

c) Die Instrumente. Für Kleintriangulierungen werden benutzt gute Nonientheodolite mit 25facher Fernrohrvergrößerung, 12–16 cm Kreisdurchmesser, Kreisteilung in ¹/₃° alter Teilung und mit 20'' Nonienangabe (bei neuer Teilung entsprechende Anordnung), oder auch Theodolite gleicher Größe mit Skalenmikroskop- oder Schraubenmikroskopablesung. Der mittlere Fehler einer in einem Satze gemessenen Richtung ist bei den erwähnten Nonien- und Skalenmikroskoptheodoliten bei sorgfältigem Verfahren erfahrungsgemäß etwa ± 5'', bei Schraubenmikroskopen etwa ± 2,5''. – Die Anzahl der Sätze wird dementsprechend zu etwa 3 bis 6 genommen. Bei der Triangulierung III. und IV. Ordnung der preußischen Landesaufnahme werden Schraubenmikroskoptheodolite von 15 cm Kreisdurchmesser angewendet, deren Mikroskope Doppelsekunden zu schätzen gestatten. – Für die Haupttriangulierungen dienen große Theodolite mit Schraubenmikroskopen. Die in [10]–[15] erwähnten Veröffentlichungen der Landestriangulierungen geben eine genaue Beschreibung der verwendeten Instrumente; eine Uebersicht über die bei den Haupttriangulierungen der Erdmessungsstaaten verwendeten Instrumente geben die Berichte von Ferrero [18] und [19]. Bei der preußischen Landestriangulierung z.B. werden für die Beobachtungen I. Ordnung Theodolite mit 27 cm Kreisdurchmesser angewendet; die Mikroskope gestatten, 0,1'' zu schätzen; der mittlere Richtungsfehler ist etwa 0,25''; für die Beobachtungen II. Ordnung dienen Instrumente mit 21 cm Kreisdurchmesser, wobei der genannte Fehler nicht über ± 1'' beträgt. Vgl. [10] und Theodolit.

d) Die Beobachtung. Bei der Ausführung der Richtungs- und Winkelmessung ist neben sorgsamer Aufstellung und Behandlung des Instruments von großer Wichtigkeit die Ausnutzung günstiger Beleuchtung und Durchsichtigkeit der Luft. Für Haupttriangulierungen sind häufig nur die späten Nachmittagsstunden als Beobachtungszeit brauchbar, weil bei greller Besonnung die Luft zittert. Auch bei Kleintriangulierungen muß in der Zeit des stärksten Flimmerns[613] die Beobachtung unterbrochen werden. Ueber Versuche, bei Haupttriangulierungen durch Nachtbeobachtungen die günstigen atmosphärischen Verhältnisse der Nacht auszunutzen und dadurch an Beobachtungszeit zu gewinnen, ist in [30] berichtet. Nach [20], Bd. 1, S. 187 und 188, sind in Nordamerika bei den Haupttriangulationen für Sichten bis 51 km mit Erfolg Acetylenlampen verwendet, vor denen je ein Paar fünfzöllige Sammellinsen aufgestellt wurde. – Instrument und Stativ sind während der Beobachtung durch starke Sonnenschirme (Beobachtungsschirme) oder durch Anbringen von Zeltleinwand an den Signalgerüsten gegen einseitige Besonnung zu schützen. Einige weitere Regeln für die Technik des Verfahrens gibt [24].

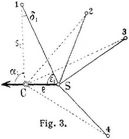
e) Die Zentrierung. In vielen Fällen ist wegen örtlicher Hindernisse, besonders bei Beobachtungsgerüsten, Stationen auf Gebäuden u.s.w., weder die Aufstellung des Instruments über dem eigentlichen Dreieckspunkte, dem Zentrum der Station, noch die Signalisierung und Anzielung des Dreieckspunktes möglich. Häufig werden sogar mehrere exzentrische Standpunkte bezw. Zielpunkte erforderlich. Diese von Nebenstandpunkten und nach Nebenzielpunkten gemessenen Richtungen oder Winkel sind dann auf das Zentrum umzurechnen, zu zentrieren. – Fig. 3 erläutert das Prinzip dieser Reduktion. Bezeichnet man das auf dem exzentrischen Standpunkt S gemessene, auf die Zentrallinie nach dem Zentrum C als Anfangsrichtung reduzierte Richtungssystem mit ε₁, ε₂, ε₃ ... ε_n und das zentrierte Richtungssystem mit α₁, α₂, α₃ ... α_n, so ist für den Zielpunkt 1 nach der Figur α₁ = ε₁ + δ₁, worin sin δ₁ = e sin ε₁ : s, oder, da δ₁ meistens ein sehr kleiner Winkel ist, δ₁ = e sin ε₁ ρ : s. Die in dieser Formel für die Ableitung von δ erforderlichen Größen e, ε und s nennt man die Zentrierungselemente, die Strecke e die Exzentrizität; diese ist möglichst scharf zu messen. Für Winkel ergeben sich die Zentrierungen als Differenzen der entsprechenden Richtungszusätze. – In ähnlicher Weise geschieht die Zentrierung für Richtungen nach Nebenzielpunkten. Weiteres über die Anordnung der Messung und Rechnung in [1] und [3]–[5]. – Ist die Exzentrizität e oder die zur Berechnung der s erforderliche Richtung zum Zentrum C nicht direkt meßbar, so sind Hilfskonstruktionen erforderlich, welche besonders bei Aufstellung auf Türmen wie kleine örtliche Triangulierungen zu behandeln sind; vgl. z.B. [1], Bd. 2, 78, und [49]. Erwähnt sei noch, daß in manchen Fällen die Berechnung von Koordinaten im Anschluß an diejenigen des Stationszentrums zweckmäßig ist. Bei kurzen Exzentrizitäten e sind besondere Vorkehrungen erforderlich. Bei Signalgerüsten kann z.B. nach Ablotung in zwei Instrumentaufstellungen die ganze Messung auf der Instrument- bezw. Leuchtplatte vorgenommen werden; vgl. hierzu [24] sowie auch [1], Bd. 2, § 78. – Nach Beilegung sämtlicher Zentrierungszusätze, zu deren Ableitung in den meisten Fällen eine vorläufige Berechnung des ganzen Netzes erforderlich ist, kann die endgültige Berechnung erfolgen.

B. Die Berechnungsarbeiten.

Der geometrische Zusammenhang für das einfache Dreiecksnetz der Fig. 1 sowie der Grundgedanke der Punktbestimmung durch Einschneiden sind eingangs angegeben worden. – Eine der hauptsächlichsten Aufgaben der Berechnung ist die Ausgleichung der unvermeidlichen Messungsfehler. Die hierzu entwickelten Rechnungsverfahren gründen sich auf der Methode der kleinsten Quadrate (s. Bd. 6, S. 415), wobei entsprechend der geometrischen Bestimmungsmethode hauptsächlich zu unterscheiden ist: Ausgleichung nach der Methode der bedingten Beobachtungen für Dreieckssysteme (Kette, Netz) und nach der Methode der vermittelnden Beobachtungen für Punktbestimmung in Koordinaten aus Richtungsschnitten. – Bei dem ersteren Verfahren sind die aus dem Netzzusammenhang sich ergebenden Bedingungen aufzusuchen und in Gleichungen auszudrücken, nachdem zuerst die Anzahl dieser Gleichungen = Anzahl der überschüssigen Bestimmungen ermittelt ist. Die Bedingungsgleichungen zerfallen in drei Arten: 1. Stationsgleichungen. Für den einfachen Fall der Fig. 1 muß die Winkelsumme der sechs Winkel um A 360° sein. Bei der Berechnung umfangreicher Netze werden die Stationsausgleichungen in der Regel für sich vorgenommen. Wenn Richtungsmessungen in vollen Sätzen vorliegen, sind die Stationsbedingungen von vornherein erfüllt. 2. Dreiecks- oder allgemein Polygongleichungen. Im Beispiel der Fig. 1 muß die Winkelsumme in jedem Dreieck 180° sein. Allgemein ist die Winkelsumme im Polygon (n – 2) 180°, wenn n die Anzahl der Winkel bedeutet. In großen Dreiecken und Polygonen ist der sphärische Exzeß (s. Bd. 3, S. 525) zu berücksichtigen. 3. Seitengleichungen. Wenn von irgendeiner Dreiecksseite, z.B. 1–2 der Fig. 1, auf irgend einem Wege durch sämtliche Dreiecke hindurch auf dieselbe Dreiecksseite zurückgerechnet wird, so muß diese Rechnung widerspruchsfrei abschließen. Durch Aufstellung und Auflösung der entsprechenden Verbesserungs- und Endgleichungen (s. Beobachtungen, bedingte, Bd. 6, S. 420) ergeben sich die den beobachteten Werten beizulegenden Verbesserungen, wodurch ein widerspruchsfreier Netzzusammenhang gewonnen wird, auf Grund dessen die Koordinatenberechnung vorgenommen werden kann. Den hierdurch angedeuteten Rechnungsgang nennt man eine Netzausgleichung, die aufzustellenden Bedingungen die Netzbedingungen.

Entsprechend gestaltet sich der Rechnungsgang, wenn ein Dreiecksnetz in ein übergeordnetes System eingeschaltet werden soll (Netzeinschaltung), z.B. in das Dreieck A–1–6 der Fig. 1 das durch gestrichelte Linien angedeutete Dreiecksnetz der Punkte 7 bis 11. Hierbei tritt zu den Bedingungen, welche in der Figur an sich zu erfüllen sind, noch die hinzu, daß das grundlegende Dreieck unverändert bleiben muß. Nach Durchführung dieser Ausgleichung können sodann aus den im übergeordneten Netz bereits festgestellten Koordinaten und Richtungswinkeln die Koordinaten der Neupunkte 7 bis 11 berechnet werden, wobei z.B. die Punkte[614] zu Polygonzügen (s. Bd. 7, S. 183) zusammengefaßt werden können und die genaue Uebereinstimmung der auf verschiedenen Wegen gewonnenen Werte eine Probe ergibt.

Für Kleintriangulierungen kann zuweilen ein vereinfachtes Ausgleichungsverfahren gewählt werden. Sind z.B. in Fig. 1 die Punkte 1 und 6 gegeben und die drei Punkte 8, 10, 11, deren Verbindungslinien Dreiecke im Zusammenhang einer Kette bilden, zu bestimmen, so hat man nach [3] und [5] den Fall des sogenannten Einkettens. Sind aber z.B. die drei Punkte 1, 8, 6 und die sie verbindenden Linien als gegeben zu betrachten und die Neupunkte 10 und 11 zu bestimmen, so hat man nach [3] und [5] den Fall des sogenannten Einschaltens. Für diese Art der bei Kleintriangulierung vorkommenden Punktbestimmungen kann dann ein vereinfachter Rechnungsgang zur Erfüllung der Bedingungen angewendet werden; vgl. [1] und [3]–[5].

Bei Haupttriangulierungen ist die Ausgleichung streng nach der Methode der kleinsten Quadrate unter Berücksichtigung der Beobachtungsgewichte durchzuführen. Der Rechnungsgang ist im übrigen der gleiche. Zum Beispiel sind für die in Fig. 4 durch starke Linien dargestellte rheinisch-hessische Kette nach Einführung der ihr angehörigen Basis die Bedingungsgleichungen aufzustellen, die sich aus der Figur ergeben. Hinzu treten die Bedingungsgleichungen aus dem Anschluß an die ältere hannoversche Kette, deren Seiten durch dicke Linien dargestellt sind. In ähnlicher Weise ist zu verfahren für das von der Kette umspannte, in dünnen Linien gezeichnete niederrheinische Dreiecksnetz, wobei zu den Bedingungen des Netzes an sich diejenigen des Randanschlusses hinzutreten. Derartige, durch gegebene Systeme umschlossene Netze werden jedoch zweckmäßiger nach der Methode der vermittelnden Beobachtungen behandelt (vgl. weiter unten).

Bei der Punktbestimmung durch Einschneiden, d.h. durch mehrfache Anwendung des einfachen und vereinten Vorwärts- und Rückwärtseinschneidens, handelt es sich darum, den wahrscheinlichsten Ort des gesuchten Punktes in Koordinaten auszudrücken.

Vorwärtseinschneiden. Soll z.B. im Gebiet des Vierecks A–2–3–4 der Fig. 1 der Neupunkt 12 durch Vorwärtseinschneiden mit den eingezeichneten Richtungen bestimmt werden, so sind zunächst die auf den vier Punkten gemessenen Richtungen r nach den aus den Koordinaten berechneten Richtungswinkeln R zu orientieren. Dies geschieht durch Zulegen des mittleren Richtungsunterschiedes [R – r] : m zu den Richtungen r. Die eckige Klammer ist das Summenzeichen, m ist die Anzahl der orientierenden Richtungen. Wenn z.B. auf Punkt 2 die Richtungen r₃, r₁₂ und r_A gemessen und die Richtungswinkel R₃ und R_A aus den Koordinaten berechnet sind, so ist die Zulage (R₃ – r₃ + R_A – r_A) : 2. Zur Ausführung der Rechnung dient ein nach [3] und [5] als Abriß bezeichnetes Schema (vgl. a. Bd. 1, S. 27). Die so gewonnenen, im Koordinatensystem orientierten, von gegebenen Punkten ausgehenden Richtungen werden als äußere Richtungen bezeichnet. Aus dem Schnitt zweier Richtungslinien, z.B. von A und 2 aus, sind nun durch einfaches Vorwärtseinschneiden (s.d.) die genäherten Koordinaten des Neupunktes 12 zu bestimmen. Danach ist der wahrscheinlichste Punktort entweder durch graphische Ausgleichung mit Hilfe einer fehlerzeigenden Figur (s. Bd. 4, S. 609) oder durch Ausgleichung nach den Regeln für vermittelnde Beobachtungen nach der Methode der kleinsten Quadrate abzuleiten. Hierbei wird für jede äußere Richtung eine sogenannte Fehlergleichung aufgestellt, welche die Beziehung zwischen Richtungs- und Koordinatenänderung ausdrückt. Auf Grund dieser Fehlergleichungen wird nach Aufstellung und Auflösung der sogenannten Endgleichungen der gefachte Punktort so bestimmt, daß die Quadratsumme der nach der Ausgleichung übrigbleibenden Richtungsfehler ein Minimum wird. Dieser hier kurz angedeutete Rechnungsgang ist der in der Kleintriangulierung übliche.

Rückwärtseinschneiden. Es soll in Fig. 1 im Gebiet des Rahmens A–12–3–4–5 der Neupunkt 13 mit den auf ihm beobachteten sogenannten inneren Richtungen bestimmt werden. In die Rechnung eingeführt werden die Koordinaten der fünf gegebenen Punkte und das beobachtete Richtungssystem. Zunächst werden aus dem Schnitt dreier Richtungen, z.B. r_A, r₄, r₅, durch einfaches Rückwärtseinschneiden (s.d.) genäherte Koordinaten des Neupunktes berechnet. Sodann wird der wahrscheinlichste Punktort entweder durch graphische Ausgleichung oder besser durch Ausgleichung nach vermittelnden Beobachtungen gewonnen; im letzten Falle ist wieder für jede beobachtete Richtung die Fehlergleichung aufzustellen und dann weiter zu rechnen, wie oben angedeutet.

Vereintes, vollständiges Einschneiden. Liegen für die Bestimmung eines Neupunktes sowohl äußere als innere (zweiseitige, doppelte) Richtungen vor, so hat man vereintes Einschneiden. Sämtliche Richtungen werden, nachdem die äußeren Richtungen orientiert sind, zusammen in die Ausgleichung eingeführt, welche wieder entweder auf graphischem Wege oder nach der Methode der vermittelnden Beobachtungen erfolgen kann. Fig. 1 zeigt in dem Rahmen A–13–5–6 die Bestimmung des Neupunktes 14 durch vereintes Einschneiden. Sind nicht, wie bisher für diese Punktbestimmung durch Einschneiden angenommen, Richtungen beobachtet, sondern einzelne Winkel, so erleidet der Rechnungsgang eine entsprechende Abänderung, [1] und [3]–[5].

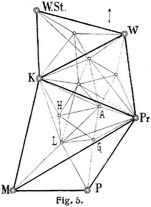
Diese hier erläuterte Einzelpunktbestimmung durch Einschneiden, wobei, wie angedeutet, vorher bestimmte Punkte (z.B. 12 und 13) als gegeben in die nachfolgende Rechnung ein geführt werden und der Gewichtsunterschied zwischen äußeren und inneren Richtungen vernachlässigt wird, ist die für Kleintriangulierungen übliche. Statt dessen können aber auch mehrere Punkte oder sämtliche Punkte eines Netzes gleichzeitig durch einheitliche Ausgleichung unter strenger Berücksichtigung der Richtungsgewichte bestimmt werden, z.B. in Fig. 5 auf Grund des in starken Linien gezeichneten Rahmens die vier Punkte H, A, G, L oder in Fig. 4 die sämtlichen Punkte des von der Kette umschlossenen niederrheinischen Netzes. Dieses letztere Verfahren wird bei Haupttriangulierungen angewendet.[615]

Die Theorie und Praxis der Triangulierungsausgleichung ist behandelt in der bei Methode der kleinsten Quadrate, Bd. 6, S. 415, genannten Literatur sowie besonders in [1]–[5]. Für die amtlichen Kleintriangulierungen gelten die für die Anordnung der Ausgleichungsrechnung erlassenen besonderen Vorschriften und Formulare, vgl. z.B. [5]. Bei den Haupttriangulierungen ist das. angewendete Ausgleichungsverfahren (Ansatz der Bedingungsgleichungen, Gewichte u.s.w.) in den Veröffentlichungen [10]–[15] speziell dargestellt.

Während bei der Kleintriangulierung die einfachen Formeln der ebenen Dreiecks- und Koordinatenberechnung Anwendung finden, tritt bei den über große Gebiete ausgedehnten Landes- und Gradmessungstriangulierungen, welche für die Kleintriangulierungen die Unterlage liefern und den wissenschaftlichen Untersuchungen der Erdmessung dienen sollen, an Stelle der ebenen Berechnungsfläche das Erdellipsoid (Bd. 3, S. 483). Es tritt daher an Stelle des ebenen Dreiecks das sphärische, das sphäroidische oder allgemein das geodätische Dreieck (s.d., Bd. 4, S. 379); an Stelle der einfachen, ebenen, rechtwinkligen Koordinaten treten die sphäroidischen und geographischen Koordinaten. – Um eine Triangulierung auf dem Erdellipsoid zu orientieren, müssen mindestens für einen Punkt (z.B. A, Fig. 1) auf astronomischem Wege der absolute Ort in geographischen Koordinaten λ, φ (s. Geographische Ortsbestimmung, Bd. 4, S. 386, und Polhöhenbestimmung, Bd. 7, S. 169) und für eine Linie (z.B. A–3) das astronomische Azimut (s. Azimutbestimmung, Bd. 1, S. 425) gemessen werden. Alsdann können nach Auflösung der sphäroidischen Dreiecke aus den Dreiecksseiten und Azimuten, von Punkt zu Punkt fortschreitend, die geographischen Koordinaten auf dem Ellipsoid berechnet werden. Das Wesentlichste über diese Aufgabe, die man als geodätische Hauptaufgabe bezeichnet, sowie die grundlegende Literatur s. Bd. 4, S. 383. Der Uebergang von diesen geographischen Koordinaten λ, φ zu den ebenen rechtwinkligen Koordinaten der Kleinmessung wird vermittelt durch die sphärischen bezw. sphäroidischen Koordinaten, welche in Bd. 5, S. 620, behandelt sind. Im übrigen muß wegen der Theorie der sphäroidischen Rechnungen auf der Erdoberfläche verwiesen. werden auf [1], Bd. 3, [2] und [7]–[9]. Außerdem geben die Veröffentlichungen der unten genannten Landes- und Gradmessungstriangulierungen [10]–[16] in der Regel die Theorie des angewendeten Rechnungsverfahrens an.

C. Anlage der Triangulierung.

Die Anordnung einer Landestriangulierung wird bedingt durch Form und Ausdehnung des Landes.

Bei der preußischen Landestriangulierung wird das Staatsgebiet durch ein weitmaschiges System von Dreiecksketten überspannt, wie die in Fig. 4 in starken Linien dargestellte rheinisch-hessische Kette; andre Ketten sind z.B. die hannoversche Kette, die hannoversch-sächsische Kette, die Elbkette, die schlesisch-posensche Kette u.s.w. Acht über das Staatsgebiet passend verteilte Grundlinien (s. Basis, Bd. 1, S. 558) liefern das Längenmaß für diese Ketten. Wegen des allmählichen Fortschrittes der Arbeit sind diese Ketten nacheinander zur Ausgleichung gelangt. Die von den Ketten umrahmten Gebiete sind durch sogenannte Füllnetze ausgefüllt, wie das niederrheinische Netz in Fig. 4; andre Füllnetze sind z.B. das schlesische, das märkische, das Wesernetz u.s.w. In die Hauptsysteme der Ketten und Netze, welche für sich geschlossen ausgeglichen werden, werden Gruppen untergeordneter Punkte und Einzelpunkte der Haupttriangulierung stufenweise eingeschaltet. Auf der Haupttriangulierung wird die Kleintriangulierung gegründet, so daß auf 10 qkm etwa zwei trigonometrische Punkte kommen. Die Berechnungsfläche ist das Besselsche Erdellipsoid (Bd. 3, S. 483, vgl. a. [10], Teil I–V), auf dem die Triangulierung durch trigonometrische Uebertragung der absoluten Position der Berliner Sternwarte und eine besondere Azimutmessung orientiert ist. Auf Grund dieser absoluten Positionen werden für sämtliche Punkte I.–IV. Ordnung geographische Koordinaten auf dem Ellipsoid berechnet, wozu die Rechnungsvorschriften amtlich festgestellt sind [43]. Während die Hauptketten und einzelne Netze nach der Methode der bedingten Beobachtungen ausgeglichen sind, werden die untergeordneten Systeme von den Füllnetzen ab, die Punktgruppen und Einzelpunkte nach Koordinaten ausgeglichen. Hierzu dient ein der preußischen Landesaufnahme eigentümliches Rechnungsverfahren. Es werden für diesen Zweck durch eine konforme Doppelprojektion die Messungen von dem Sphäroid auf eine Rechnungskugel und von dieser auf die Ebene und wieder zurück übertragen; vgl. hierüber [44]–[46] sowie Bd. 5, S. 622. Wegen der Landestriangulierungen der andern Staaten s. [10]–[15]. Eine zusammenfassende kritische Darstellung bis 1882 gibt [16], eine gute Uebersicht [1], Bd. 1, Kap. 4. Ueber den Stand der Landestriangulierungen in den zur internationalen Erdmessung (Bd. 3, S. 483) gehörenden Staaten wird fortlaufend berichtet in den Protokollen und Verhandlungen der internationalen Erdmessung. Ausführliche Berichte geben Ferrero in [18] und [19] sowie Helmert und Krüger in [20]. Eine Zusammenstellung der gesamten internationalen Literatur bis 1889 s. in [21]. Eine kurze Uebersicht über die besonderen, für Gradmessungszwecke (Breiten- und [616] Längengradmessungen) ausgeführten Triangulierungen gibt [47], das Wesentlichste auch [1], Bd. 1 und 3. Einige der wichtigsten älteren Gradmessungstriangulierungen in Deutschland neben den in [10]–[15] genannten sind die hannoversche Gradmessung von Gauß, vgl. hierzu [25] mit Literaturangaben, die ostpreußische Gradmessung von Bessel und Baeyer [22], das rheinische Dreiecksnetz des Preußischen Geodätischen Instituts [23]. Ueber die Bedeutung der Triangulierungen für die Bestimmung und Untersuchung der Erdfigur s. Erde, Bd. 3, S. 480. Wegen einer kolonialen Grenzvermessungstriangulierung s. [31].

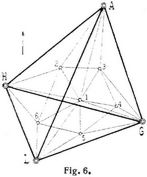
Die als Unterlage für die Spezialvermessungen erforderlichen Kleintriangulierungen sind eine Fortführung der Landestriangulierung, wobei nur entsprechend ihrem Zweck besondere Rücksicht auf den sicheren Anschluß der Kleinmessungen zu nehmen ist; z.B. ist besonders wichtig, daß benachbarte Punkte, welche durch Polygonzüge und Messungslinien verbunden werden, im Zusammenhang bestimmt werden. Die Einführung zweckmäßig angeordneter Berechnungsflächen s. Bd. 5, S. 620. Wegen der die Regel bildenden Einzelpunktausgleichung nach Koordinaten ist eine zweckmäßige Punktfolge hierbei von großer Wichtigkeit; im allgemeinen soll der jeweils zu bestimmende Neupunkt etwa im Schwerpunkt des ihm unmittelbar übergeordneten feststehenden Rahmens liegen und durch Richtungen nach 3–6 gegebenen Punkten mit etwa 4–12 bestimmenden (äußeren oder inneren) Richtungen (am besten Doppelrichtungen) berechnet werden. In [49] ist ein Schema für die Anordnung des Rechnungsganges mitgeteilt, welches gleichzeitig den Plan für die Richtungsmessung, die Punktfolge und die Ausgleichung gibt. Ein Beispiel für die Anordnung einer Kleintriangulierung zeigt Fig. 6. Sie zeigt eine für die Zwecke der Spezialvermessungen entworfene Triangulierung, welche durch Vermittlung des in Fig. 5 dargestellten Netzes sich auf den in Fig. 4 unten links durch Buchstaben bezeichneten Teilen der Kette und deren Zwischenpunkten gründet. Weiteres über die Anordnung der Kleintriangulierungen s. [1] und [3]–[5]. Für die amtlichen Triangulierungen der Katastervermessungen gelten die betreffenden Vorschriften in den bei Kataster (Bd. 5, S. 404) genannten Anweisungen. Eine Uebersicht über die Anordnung der amtlichen Kleintriangulierungen gibt [16], Bd. 2. Ueber die Triangulierung des deutschen Kiautschougebiets s. [32]. Für städtische Triangulierungen sei verwiesen auf [1], Bd. 2, [33]–[39], sowie die zahlreichen Artikel in den Fachzeitschriften, worüber die jährlichen Literaturberichte der Zeitschrift für Vermessungswesen [6] eine Uebersicht geben. Beispiele besonderer Triangulierungen für den Bau des Gotthardtunnels und des Simplontunnels finden sich in [40] und [41]. Wegen der trigonometrischen Grundlagen für Eisenbahnvorarbeiten s. [1], Bd. 2. Ueber die bei der preußischen Landesaufnahme eingeführte Bestimmung der sogenannten Leit- und Folgepunkte s. [42] und [1], Bd. 1, Kap. 3. – Ueber graphische Triangulierung bei der Meßtischaufnahme s. Bd. 6, S. 394.

D. Ergebnisse und Genauigkeit der Triangulierungen.

Die Ergebnisse der Landestriangulierungen sind die Richtungswinkel auf den Stationen und die Entfernungen nach den benachbarten Punkten, welche aus Beobachtung und Ausgleichung hervorgegangen sind, d.h. Polarkoordinaten, und die geodätisch abgeleiteten geographischen Koordinaten, Länge λ, Breite φ. Bei der preußischen Landestriangulation kommen die konformen Rechnungskoordinaten hinzu, welche jedoch nicht für den öffentlichen Gebrauch ohne weiteres geeignet sind.

Die Ergebnisse der Landestriangulierungen sind veröffentlicht in den unter [10]–[15] und [18]–[23] genannten Werken. Für die Zwecke der amtlichen Spezialvermessungen werden aus den geographischen Koordinaten, welche für die topographischen Arbeiten direkte Verwendung finden, rechtwinklige Koordinaten abgeleitet (s. Bd. 5, S. 620), so daß die Ergebnisse der Kleintriangulierungen sind: rechtwinklige Koordinaten, beobachtete und ausgeglichene Richtungswinkel in dem betreffenden Koordinatensystem und die Entfernungen zu den benachbarten Punkten. Die Ergebnisse der Triangulierungen für die Spezialvermessungen werden bisher nur teilweise veröffentlicht, sind aber stets von den betreffenden Behörden zu erfahren.

Die Genauigkeit der Triangulierungen ist nach älteren Bestimmungen bei Haupttriangulierungen als genügend zu betrachten, wenn die wahrscheinlichen Fehler der Seiten nicht über 0,00001 der Länge hinausgehen, während für die Kleintriangulierung die Genauigkeit von 0,00004 der Länge genügt. Zurzeit läßt sich der Fehler der Basismessung etwa innerhalb 0,000001 der Länge halten und der Fehler einer auf der Station ausgeglichenen Richtung bei Anwendung der erwähnten großen Instrumente mit Schraubenmikroskopablesung unter 0,5'' a. T. Bei der preußischen Landestriangulierung ist der Fehler neuerdings nicht größer als 0,25''. Als Ausdruck für die Genauigkeit einer Triangulierung dient der mittlere (bezw. wahrscheinliche) Fehler einer Richtung oder eines Winkels, wobei zu unterscheiden ist zwischen dem aus der Stationsausgleichung berechneten reinen Messungsfehler, dem aus den Dreiecks- bezw. Polygonwidersprüchen abgeleiteten sowie dem aus der Netzausgleichung mit etwaigem Anschlußzwang sich ergebenden Fehler. Als Vergleichswert für die Genauigkeit der internationalen Triangulierungen ist seitens der internationalen Erdmessung [48] der aus den[617] Dreiecksschlußwidersprüchen w sich ergebende Wert m nach der sogenannten internationalen Formel

eingeführt, worin die eckige Klammer das Summenzeichen und n die Anzahl der Dreiecke bedeuten. In [18], [19] ist für die wesentlichsten Triangulierungen der Erdmessungsstaaten die Genauigkeit angegeben. Für die bellen Triangulierungen ist m rund 0,5''. Die aus den Netzausgleichungen sich berechnenden Fehler sind im allgemeinen größer, rund 1,5 mal so groß. In den unter [10]–[15], [22] und [23] genannten Veröffentlichungen sind weitere spezielle Fehleruntersuchungen enthalten, auf welche hier nur verwiesen werden kann. Eine Uebersicht gibt [1], Bd. 1, S. 526. Der Fehler der Punktabstände auf der Berechnungsfläche ist bei guten Haupttriangulierungen für 30–60 km Abstand nicht über 1 dm, sehr häufig erheblich geringer. Der exakte Ausdruck für den Punktortfehler ist die Fehlerellipse (s. Bd. 3, S. 666). – Für Kleintriangulierungen ist der Fehler der Punktabstände unter der Voraussetzung der erwähnten Genauigkeit für das übergeordnete Netz bei Abständen bis zu 1 km, 0,75 oder 0,5 km auf rund einige Zentimeter bis höchstens 1 dm zu schätzen. Die Innehaltung dieser Genauigkeit wird im allgemeinen gesichert durch Fehlergrenzen für die Abweichung zwischen den endgültig ausgeglichenen und den beobachteten Richtungen. Bei den preußischen Katastervermessungen gilt z.B. für Triangulierung III. Ordnung als Fehlergrenze 15'', für IV. Ordnung 25'', V. Ordnung 35''. Zu diesen Abweichungen tragen etwa je zu einem Drittel bei die Fehler der gegebenen Punkte, die Fehler der Richtungs- bezw. Winkelmessung und die Fehler der Zentrierung der Instrumente und Signale. Wegen der Ausführung dieser Fehlerberechnungen für Kleintriangulierungen s. [49], [50]; Ergebnisse von Genauigkeitsbestimmungen für Kleintriangulierungen sind weiter mitgeteilt in [33]–[39]. Nach dem Zweck und der Genauigkeit, die erreicht werden soll, müssen die Punktbestimmung, Signalisierung, Beobachtung, Ausgleichungs- und Rechnungsverfahren und die Rechnenschärfe bemessen werden. Für städtische Kleintriangulierungen ist z.B. zu beachten, daß Kirchtürme, welche äußerst geeignete und vielseitig verwendbare Zielpunkte abgeben, die Punktorte zum Teil nur wenig scharf bezeichnen und unvermeidlichen kleinen Lageänderungen ausgesetzt sind, so daß hierdurch von vornherein eine gewisse Grenze für die Genauigkeit der Punktorte gegeben ist.

Literatur: Die Grundzüge der Triangulierung sind behandelt in den bei Geodäsie (Bd. 4, S. 378) unter [4]–[10] genannten Lehrbüchern der Geodäsie. Die eingehendste Behandlung mit Rücksicht auf Theorie und Praxis gibt [1] Jordan, Handbuch der Vermessungskunde, Stuttgart, Bd. 1, 5. Aufl., Reinhertz, 1904; Bd. 2, 7. Aufl., Reinhertz, fortgesetzt von Eggert, 1908; Bd. 3, 5. Aufl., Reinhertz, 1907. – [2] Hegemann, Lehrbuch der Landesvermessung, Berlin 1906. – Als Spezialschriften für das Rechnungswesen der Kleintriangulierung sind zu nennen: [3] Gauß, F.G., Die trigonometrischen und polygonometrischen Rechnungen in der Feldmeßkunst, 3. Aufl., 2 Bände, Halle 1906; ferner auch [4] Franke, Dreiecksnetze IV. Ordnung, München 1871, und Franke, Grundlinien der trigonometrischen Vermessung, Leipzig 1879. – Als amtliche Anweisung für das Rechnungswesen der Kleintriangulierung sei verwiesen auf [5], IX. Anweisung für die trigonometrischen und polygonometrischen Arbeiten bei Erneuerung der Karten und Bücher des Grundsteuerkatasters, 3. Aufl., Berlin 1903 (vgl. auch die Literatur zu Kataster, Bd. 5, S. 409). – Ueber die zahlreichen einschlägigen Aufsätze in den Fachzeitschriften geben eine Uebersicht die [6] jährlichen Literaturberichte der Zeitschr. f. Vermessungswesen, Stuttgart. – Die Theorie der sphärischen und sphäroidischen Triangulierung auf der gekrümmten Erdoberfläche ist behandelt in [7] Helmert, Die mathematischen und physikalischen Theorien der höheren Geodäsie, Bd. 1: Die mathematischen Theorien, Leipzig 1880, sowie in [1] Jordan, Bd. 3. – Eine empfehlenswerte übersichtliche Darstellung geben auch [8] Zachariae, Die geodätischen Hauptpunkte, deutsch von Lamp, Berlin 1878. – [9] Clarke, Geodesy, Oxford 1880. – Einige der wichtigsten Veröffentlichungen über die Landestriangulierungen in Deutschland sind [10] Kgl. Preußische Landestriangulation, Hauptdreiecke, Teil I–XI, Berlin 1870–1901; ferner das die Ergebnisse darstellende, in 24 einzelnen Bänden nach Verwaltungsgrenzen erscheinende Werk [11] Kgl. Preußische Landestriangulation, Polarkoordinaten, geographische Positionen und Höhen (Titel der älteren Bände), Abrisse, Koordinaten und Höhen (Titel der neuen Bände), Teil 1–20, Berlin 1874–1908; fortlaufende Berichte über das Erscheinen der Werke in [6]. – [12] Die bayerische Landesvermessung in ihrer wissenschaftlichen Grundlage, München 1873, und Die bayerische Landesvermessung in ihrer geschichtlichen Entwicklung, München 1908. – [13] Kohler, Die Landesvermessung des Königreichs Württemberg in wissenschaftlicher, technischer und geschichtlicher Beziehung, Stuttgart 1858. – [14] Astronomisch-geodätische Arbeiten für die europäische Gradmessung im Königreich Sachsen, 1. Abteil.: Die Großenhainer Grundlinie, Berlin 1882; 2. Abteil.: Das trigonometrische Netz, Berlin 1890. – [15] Großh. Mecklenburgische Landesvermessung, 4 Teile, Schwerin 1882; 5. Teil, 1895. – Weiteres über die deutschen Landesvermessungstriangulierungen gibt bis 1882 [16] Jordan-Steppes, Das deutsche Vermessungswesen, 2 Bde., Stuttgart 1882. – Ueber diese sowie die internationalen Arbeiten geben Auskunft [17] die Veröffentlichungen der internationalen Erdmessung bezw. der europäischen Gradmessung, Verhandlungen, Protokolle u.s.w., sowie auch [18] Internationale Erdmessung, Verhandl. zu Brüssel 1892; Ferrero, Rapport sur les triangulations (besonderer Band). – [19] Ebend., Berlin 1895, Bd. 2, A. 3. – [20] Ebend., Kopenhagen 1903, Bd. 2, B. 13. – [21] Internationale Erdmessung, geodätische Literatur, zusammengestellt von Börsch, Berlin 1889. – [22] Bessel u. Baeyer, Gradmessung in Ostpreußen, Berlin 1838. – [23] Veröffentlichungen des Geodätischen Instituts, Das rheinische Dreiecksnetz, Heft 1, Berlin 1876; Heft 2, 1878; Heft 3, 1882. – [24] Kgl. Preußische Landestriangulation, Triangulation II. Ordnung der Umgegend von Berlin, Berlin 1867. – [25] Gaede, Beiträge zur Kenntnis von Gauß' praktisch-geodätischen Arbeiten, Zeitschr. f. Verm. 1885, S. 113. – [26] Erfurth, Technischer Betrieb der Feldarbeiten der Triangulation I. Ordnung, Zeitschr. f. Verm. 1887, S. 377. – [27] Paschen, Astronom. Nachr., Nr. 1492/93. – [28] Vogler, Stationsbeobachtungen in symmetrischer[618] Anordnung, Zeitschr. f. Verm. 1885, S. 49. – [29] Schreiber, Anordnung der Horizontalwinkelbeobachtungen auf der Station, Zeitschr. f. Verm. 1878, S. 209; Ders., Richtungsbeobachtungen und Winkelbeobachtungen, ebend. 1879, S. 97. – [30] Werner, Winkelmessung bei Tag und Nacht, Zeitschr. f. Instrumentenk. 1883, S. 225. – [31] Bericht über die Grenzvermessung zwischen Deutsch-Südwestafrika und Britisch Bechuanaland, Berlin 1906. – [32] Die Vermessung des deutschen Kiautschougebiets, Berlin 1901. – Für städtische Triangulierungen sei verwiesen auf [33] Jordan, Triangulierung des Stadtbezirks Hannover, Zeitschr. f. Verm. 1892, S. 1. – [34] Harksen, Haupttriangulation für den Stadtkreis Remscheid, Zeitschr. f. Verm. 1895, S. 153. – [35] Händel, Vermessung der Stadt Leipzig. Zeitschr. f. Verm, 1895, S. 100; vgl. a. die bei Stadtvermessung genannte Literatur. – [36] Gerke, Triangulation und Polygonisierung der Stadt M.-Gladbach, Hannover 1885. – [37] Stück, Das hamburgische Vermessungswesen, 3. Teil, Hamburg 1886. – [38] Vermessung der Freien Hansestadt Bremen; Geißler, Triangulation II. Ordnung, Bremen 1890; III. Ordnung, 1891; IV. Ordnung, 1894. – [39] Das Vermessungswesen der Kgl. Haupt- und Residenzstadt Dresden, Triangulation I., II., III. Ordnung, Dresden 1896. – [40] Koppe, Bestimmung der Achse des Gotthardtunnels, Zeitschr. f. Verm. 1875, S. 369; 1876, S. 86, 129 u.s.f. – [41] Rosenmund, Spezialberichte der Direktion der Jura-Simplonbahn an das schweizerische Eisenbahndepartement über den Bau des Simplontunnels, Bern 1901. – [42] Jordan, Bestimmung eines Folgepunktes bei der trigonom. Abteilung der Landesaufnahme, Zeitschr. f. Verm. 1889, S. 1. – [43] Rechnungsvorschriften für die trigonometrische Abteilung der Landesaufnahme, Formeln, Tafeln u.s.w., I., II., III. Ordnung, Berlin 1878. – [44] Schreiber, Die konforme Doppelprojektion der trigonometrischen Abteilung der preußischen Landesaufnahme, Berlin 1897. – [45] Schreiber, Theorie der Projektionsmethode der hannoverschen Landesvermessung, Hannover 1866. – [46] v. Schmidt, Projektionsmethode der trigonom. Abteilung der Kgl. Preuß. Landesaufnahme, Zeitschr. f. Verm. 1894, S. 385. – [47] Sadebeck, Der Entwicklungsgang der Gradmessungsarbeiten, Berlin 1876. – [48] Internationale Erdmessung, Verhandlungen in Nizza 1887, Berlin 1888, S. 54. – [49] Reinhertz, Die Verbindungstriangulation zwischen dem rheinischen Dreiecksnetz der europäischen Gradmessung und der Triangulation des Dortmunder Kohlenreviers der preußischen Landesaufnahme, Stuttgart 1889. – [50] Ders., Einige Bemerkungen über Kleintriangulierung, Zeitschr. f. Verm. 1892, S. 452.

(† Reinhertz) Hillmer.

Fig. 1.

Fig. 2.

Fig. 3.

Fig. 4.

Fig. 5.

Fig. 6.