Tachymetrie
[403] Tachymetrie, Tacheometrie, Celerimensura, Schnellmessung, ein Messungsverfahren, bei dem die Lage- und Höhenmessungen gleichzeitig ausgeführt werden durch Bestimmung der Horizontalrichtungen, durch Distanzmessung (s. Distanzmesser) sowie durch Beobachtung von Höhen- oder Zenitwinkel oder durch unmittelbare Messung der Höhenunterschiede. Die zweckmäßige Vereinigung dieser Messungen führt gegenüber andern Verfahren eine Zeitersparnis herbei, woraus sich die Namen erklären, doch tritt die Zeitersparnis im allgemeinen ein auf Kosten der Genauigkeit. Nach den Instrumenten, die benutzt werden, unterscheidet man Theodolit-, Bussolen- und Meßtischtachymetrie und nach der Art der Ausführung Zahlentachymetrie und graphische Tachymetrie. Wird die Genauigkeit der Zahlentachymetrie so gesteigert, daß die Längenbestimmung der sorgsam ausgeführten Latten- oder Meßbandmessung gleichwertig wird, so nennt man das Verfahren Präzisions- oder Feintachymetrie. Die Tachymetrie ist von großer Bedeutung für geometrische Vorarbeiten. Sie verdankt ihre Entwicklung namentlich dem Eisenbahnbau.[403] Die Instrumente heißen in Deutschland und Nordamerika Tachymeter, in Frankreich und England Tacheometer, in Italien Celerimeter. Auch findet man die Namen Omnimeter, Stadimeter, Euthimeter, Viel- und Schnellmesser u.a. Die Instrumente sind mannigfacher Art. Sie unterscheiden sich einerseits nach ihren Einrichtungen für die Distanzmessung, anderseits nach ihren Anordnungen als Theodolit, Bussole oder Meßtisch für die Bestimmung der Horizontalrichtungen. Das Tachymeter in Verbindung mit dem Meßtisch nennt man Tachygraphometer.
I. Die tachymetrischen Instrumente.
1. Tachymeter mit Höhenkreis- und Okularfadendistanzmesser. Die größte Bedeutung hat der mit Höhenkreis und seiten Distanzfäden im Fernrohr ausgerottete Theodolit. Eine Repetitionseinrichtung am Theodolit gewährt manche Vorteile. Wesentlich ist ein gutes Fernrohr von etwa 25–35 facher Vergrößerung, dessen Distanzkonstante eine runde Zahl, in der Regel 100, 200 oder auch 50, ist. Das Fadennetz ist entweder auf Glas eingerissen (Glasmikrometer) oder besteht aus aufgespannten Spinnfäden und ist zuweilen justierbar (s. Fadennetz, Bd. 3, S. 562 und [4]. Weiteres über die Fadendistanzmesser, Bestimmung der Konstanten u.s.w. s. Bd. 2, S. 783, sowie die dort angegebene Literatur). Die Kreisablesung soll möglichst bequem sein; für die meisten Fälle genügt die Genauigkeit eines kleinen Theodolits (vgl. [5]). Neben den üblichen Nonienangaben (s. Nonius, Bd. 6, S. 657) von 1/2' oder 1/3' ist zweckmäßig Kreisteilung in 1/6° und einfache Schätzung der Minuten an einem Indexstrich mit Hilfe einer starken offenen Lupe. Entsprechend wird die Anordnung bei Zentesimalteilung getroffen. Auch mikroskopische Ablesung findet Anwendung, z.B. bei dem unten beschriebenen Cleps [6]–[8], dem Tachymeter mit Strichmikroskop von Fennel [10] und bei dem logarithmischen Tachymeter von Tichy und Ott [11]. Letzteres hat außerdem für die Distanzmessung ein Glasmikrometer mit 11 Vertikalstrichen, 1 Horizontalstrich und 1 Transversalstrich, von Tichy optischer Meßkeil genannt. Zur Messung der Höhenwinkel dient entweder ein Vollkreis, ein Doppelbogen oder ein einfacher Bogen mit einem Zeiger oder zwei Zeigern (vgl. Fig. 1–5). Die Teilung entspricht derjenigen des Horizontalkreises; für die Bezifferung sind am bellen Zenitwinkel (z); Höhenwinkel (± α) geben leicht Anlaß zu Vorzeichenfehlern. Bei einzelnen Instrumenten kommen nebenher besondere Teilungen des Höhenkreises vor, z.B. Gefällprozentteilung bei [12], Teilung nach sin α cos α bei einem Tachymeter von Goulier [13], S. 427, eine logarithmische Teilung bei [11]. Die Höhenkreislibelle wird entweder am Fernrohrträger oder besser am Zeigerträger mit besonderem Feinstellarm (z.B. Fig. 3) angebracht. Häufig ist, der Genauigkeit der Ablesung entsprechend, für Horizontal- und Vertikalkreis nur je ein Zeiger vorhanden; besser sind für die Prüfung des Instrumentes sowie für die Bestimmung wichtiger Punkte, z.B. im Tachymeterzug (s. II), zwei Zeiger. Wegen der Prüfung und Berichtigung des Instrumentes s. Höhenwinkel, Bd. 5, S. 98, und Theodolit sowie [1]. In der Regel ist dem Instrument eine Bussole beigegeben, und zwar entweder eine Kreisbussole, welche unmittelbar über dem Theodolitkreis liegt (Fig. 3) oder als Aufsatzbussole (Fig. 4) konstruiert ist, oder auch ein Kasten- oder Röhrenkompaß zur Einrichtung des Horizontalkreises in eine konstante Stellung zur magnetischen Achse der Nadel. Bei kleinen Instrumenten, die zu Arbeiten geringer Genauigkeit dienen sollen, ist überhaupt kein Horizontalkreis, sondern nur eine Bussole vorhanden (Tachymeterbussole). Nach Bd. 2, S. 783, Formel 4. ist die allgemeine Gleichung für die Entfernung beim Fadendistanzmesser, wenn die Ziellatte rechtwinklig zur Mittelzielung steht, D = a + k L, worin L der Lattenabschnitt und a und k die der Einrichtung des Fernrohrs entsprechenden Konstanten sind; beim sogenannten anallaktischen Fernrohr nach Porro ist a = 0. Vgl. a. [1], S. 739. In Deutschland ist am verbreitetsten die alte Reichenbachsche Einrichtung mit Ramsdenschem oder orthoskopischem Okular, seltener die Ertelsche mit Huyghenschem Okular. Vgl. hierzu auch [14]. Daneben findet aber auch das Porrosche Fernrohr Anwendung, besonders bei den italienischen Instrumenten von Salmoiraghi in Mailand [6], den Tachymetern von Starke und Kammerer in Wien und verschiedenen französischen Instrumenten [13].
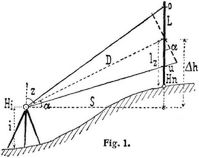
Beim einfachen Fadendistanzmesser Reichenbachscher Anordnung ist nach Fig. 1 bei lotrecht eingerichteter Distanzlatte und Einführung von Höhenwinkeln α für alle praktischen Rechnungen genügend genau S = D cos α = L k cos2 α + a cos α; beim Porroschen Fernrohr mit a = 0 wird S = L k cos2 α; diese Form reicht auch häufig bei topographischen Aufnahmen für die Reichenbachsche Einrichtung aus. Eine bessere Näherung gibt S = L k cos2 α + a, wobei a oder eine andre Konstante für mittleres α im Kopf dem berechneten Werte zugelegt wird, oder die Form S = (L k + a) cos2 α = (k + a : L) L cos2 α = k' L cos2 α, worin k' eine auf ein mittleres L bezogene Konstante bedeutet. Wird, hauptsächlich nur bei Schiebetachymetern, s. unten, die Latte rechtwinklig zur Ziellinie gerichtet, so ist S = (L k + a) cos α + lz sin α, wobei lz den Abstand der Mittelfadenablesung vom Lattenfußpunkt bedeutet. Zur lotrechten Einrichtung der Latte über dem Messungspunkt dient eine Dosenlibelle (vgl. Bd. 6, S. 648, Fig. 15); zur Einrichtung der Latte rechtwinklig zur Ziellinie benutzt man ein Diopter. Der Einfluß des Fehlers der Lattenstellung (sogenannte Lattenschiefe) auf die Größe L und damit auf die Entfernung wächst mit der Neigung der Ziellinie gegen die Lattenrichtung, ist also bei rechtwinklig[404] zur Ziellinie eingerichteter Latte im allgemeinen kleiner als bei lotrechter. Anderseits ist die lotrechte Stellung der Latte mit Hilfe der Dosenlibelle verhältnismäßig leicht und genau herzustellen und innezuhalten, so daß bei den in der Praxis vorwiegenden geringen Neigungen der Unterschied außer Betracht bleibt. Dementsprechend wird die Lotrechtstellung der Latte allgemein vorgezogen; vgl. hierüber [15] und [1]. Ueber den Einfluß der Lattenschiefe s.a. [16]. Strengere Formeln für die Entfernung s. in [1]. – Der Höhenunterschied Δ h des Zielpunktes an der Distanzlatte, auf den die mittlere Absehlinie gerichtet ist, gegen die Instrumentachse Hi ist bei dem einfachen Fadendistanzmesser nach Fig. 1 Δ h = D sin α = S tg α = L k sin α · cos α + a sin α; wenn a = o oder a sin α außer Betracht bleibt, ist Δ h = 1/2 L k sin 2α oder wie oben = 1/2L k' sin 2α. Ferner ist Hn + lz = Hi + Δ h, wenn Hn die Höhe des Punktes bedeutet, auf dem die Latte steht. Daraus kann, wenn Hi gegeben ist, die Höhe Hn, und wenn Hn gegeben ist, die Höhe Hi berechnet werden. Steht das Instrument zentrisch über einem gegebenen Höhenfestpunkt Hp, so kann der Abstand i der Instrumentachse vom Festpunkt direkt gemessen werden, Hi = Hp + i. Wird dann lz = i gemacht durch Anbringung einer Zielscheibe, so bleiben beide Werte außer Betracht, indem Hn = Hp + Δ h ist; gleiches ist der Fall, wenn Hi von einem gegebenen Festpunkte abgeleitet und lz hierbei und bei allen andern Ablesungen konstant, z.B. Im oder 2 m, genommen wird. Für Lattenstellung rechtwinklig zur Ziellinie ist Δ h = (L k + a) sin α. Das über die Berechnung der Höhen Gesagte gilt, wenn statt h der Wert lz cos α eingeführt wird. Der Einfluß der Erdkrümmung und Refraktion bleibt bei der tachymetrischen Höhenmessung außer Betracht Er wird nur bei langen Sichten nach entfernten trigonometrischen Höhenpunkten berücksichtigt, vgl. Bd. 5, S. 92.
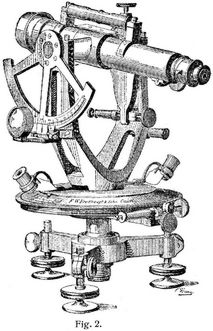
Die Fig. 2–4 zeigen einige der bemerkenswertesten Formen des einfachen Theodolittachymeters. Fig. 2 ist ein Instrument nach Puller [17] von Breithaupt; es ist nur das unbedingt Notwendige angebracht.
Fig. 3 zeigt ein für die Akademie Bonn-Poppelsdorf von Wolz konstruiertes Instrument. Es hat einen Höhenkreis mit Zylinderteilung, ein Fernrohr mit Objektivtrieb; der Zeiger des Horizontalkreises befindet sich unter dem Fernrohrokular, die Vertikalkreislibelle ist mit Ablesespiegel versehen. Durch diese Anordnung kann der Beobachter sämtliche Ablesungen für Geländepunkte vom Fernrohrokular aus nehmen, ohne den Platz zu ändern. Zugaben sind eine zwischen den Fernrohrträgern einschiebbare Bussole (Schmalkalder mit zylindrischer Kreisteilung) und eine Tangentenkippschraube (Konstante 1 : 100) an der Fernrohrfeinstellung für gelegentliche Distanz- und Höhenmessung ohne Benutzung der Distanzfäden (s. unten).
Fig. 4 ist die Abbildung eines Theodolittachymeters mit Aufsatzbussole von Hildebrand. Nach Mitteilung der Firma ist dieses Instrument in mehreren Tausenden von Exemplaren im Gebrauch. – Andre Anordnungen des Theodolittachymeters s. in [1] sowie in den Verzeichnissen der Bd. 4, S. 382, genannten mechanischen Institute.
Eine besondere Einrichtung hat ein als Cleps oder Clepscykel bezeichneter Instrumenttypus von Salmoiraghi in Mailand. Die beiden Kreise haben kleine Durchmesser von 3,5–6 cm. Sie sind, wie der Name anzeigt, in einem Kasten eingeschlossen. An der Seite des Kastens lind stark vergrößernde Mikroskope für die Kreisablesungen angebracht. Eine andre Eigentümlichkeit: ist das stark vergrößernde Fernrohr, dessen Glasmikrometer zur Verschärfung der Entfernungsbestimmung mehrere einander entsprechende Strichpaare aufweist. Diesen sind besondere Okulare zugeordnet (s. Argusokular).[405]
2. Tachymeter mit Höhenkreis und Okularmikrometerdistanzmesser. Durch die Verwendung dieses Distanzmessers wird eine Verschärfung der Messung angestrebt. (Näheres s. Bd. 2, S. 784.) Er ist hauptsächlich verwendet bei den Tachymetern von Starke und Kammerer und wird empfohlen in [18]. Für die Feintachymetrie ist bestimmt das Tachymeter Patent Tichy und Starke [7]. Der Höhenkreis hat außer der Gradteilung zwei tachymetrische Teilungen nach Funktionen des Höhenwinkels α. Diese zeigen die Stellung des Okularmikrometers an, bei denen die horizontale Entfernung und der Höhenunterschied das 100 fache der entsprechenden Lattenabschnitte sind. Ebenso dient der Feintachymetrie das logarithmische Universaltachymeter Patent Tichy und Starke in Verbindung mit einer logarithmisch geteilten Latte, die den Vorteil bietet, daß die Intervalle in den verschiedenen Entfernungen gleichgroß erscheinen. Zur Ausführung der Rechnung lind besondere Tabellen vorhanden [19]. Ohne Benutzung der Tafeln kann die horizontale Entfernung mit Hilfe einer besonderen logarithmischen Teilung des Höhenkreises bestimmt werden.
3. Tachymeter mit Schrauben-, Skalenmikrometer-, Kontakt- und Hebeldistanzmessern, teils mit, teils ohne Höhenkreis. Die Bedeutung der Fadendistanzmesser, die sich für die Tachymetrie besonders eignen, haben diese Distanzmesser nicht erlangt. (Näheres über sie s. Bd. 2, S. 785.) Für lotrechte und wagerechte Tangentenschrauben gilt nach den Fig. 6 und 7 in Bd. 2, S. 785 S = L d : p = L d : g σ, wenn g die Ganghöhe und σ die Anzahl der Umdrehungen der Schraube bedeuten. Wird eine konstante Lattenlänge L gewählt, so ist S = k1 : σ; Teilumdrehungen werden an der geteilten Schraubentrommel ermittelt. Wenn dagegen die Schraubenbewegung konstant genommen wird, so ist S = k2 L; k2 muß eine bequeme Konstante, etwa 100 sein. Ferner ist nach den Beziehungen der Figuren Δ h = (u – h)L : (o – u) oder, wenn für u – h und o – u die geraden Anzahlen von Umdrehungen σ1 und σ2 gewählt werden, Δ h = σ1 L : σ2. Wird für σ2 eine Umdrehung genommen, so ist Δ h = σ1 L. Diese Formeln gelten auch für den Theodolit mit Tangentenschraube, wenn der Mitnehmer zur Absehlinie rechtwinklig steht. Muß die Absehlinie erheblich geneigt werden, so wird die Schraubenbewegung auf den mikrometrischen Winkel beschränkt und der Höhenwinkel α berücksichtigt. Wenn α sich auf die obere Sicht bezieht, so ist S = k1 cos2 α : σ + L sin σ cos σ = k2 L cos2 α : σ + L sin σ cos σ und Δ h = S tg α oder Δ h = k1 sin α cos α : σ + L sin2 σ = k2 L sin α cos α + L sin2 α. Die zweiten Glieder der rechten Seiten können häufig vernachlässigt werden. Auch kann gesetzt werden sin α cos α = 1/2 sin 2α. Die lotrechte Tangentenschraube findet man hauptsächlich bei Nivelliertachymetern, z.B. bei den Instrumenten von Hogrewe [20] und Breithaupt [21], sodann auch bei Meißners Patenttangententachymeter, s. [1], S. 727, und die da angegebene Literatur. Die wagerechte Tangentenschraube ist angewendet beim Nivellier von Decher [22]. An der Fernrohrfeinstellung des Theodolittachymeters angebracht, ermöglicht sie neben der Fadendistanzmessung auch die Schraubendistanz- und Höhenmessung mit konstantem oder veränderlichem Schraubenintervall, was für manche Fälle Vorteile bietet; s. Fig. 3. Sie ist besonders in Amerika in Gebrauch gekommen. Eine solche Schraube neben einem Porroschen Distanzmesser hat das Tachymeter Klingatsch-Rost [23]. Durch eine besondere Vorrichtung wird die obenerwähnte Beschränkung der Schraubenbewegung auf den mikrometrischen Winkel erreicht bei dem Universaltacheograph von Ziegler-Hager [24]; s.a. Bd. 2, S. 786. Ueber eine ein gehende Würdigung der Tangentenschraube s. [25]. – Die annähernd lotrecht wirkende Sehnenschraube ist von Stampfer eingeführt; s. hierüber Bd. 2, S. 785 und die da angegebene Literatur, sowie Bd. 6, S. 644. Näherungsweise gelten die für die Tangentenschraube angegebenen Formeln auch für die Sehnenschraube. Ueber streng richtige Formeln s. die angegebene Literatur. – Bei einigen Instrumenten ist das Schraubenmikrometer durch ein Skalenmikrometer ersetzt worden, z.B. bei Hahns Universalhöhen- und Distanzmeßinstrument und bei Gordians Nivellierinstrument; s. Bd. 2, S. 786 und die da angegebene Literatur. Mikroskopablesung an einer horizontalen Tangentenskala und Verfeinerung der Ablesung durch mikrometrische Verschiebung der Skala ist eingerichtet an Eckholds Omnimeter [26]; s.a. Bd. 2, S. 786 und Fig. 7 auf S. 785. Hiernach ist Δ ho = o S : d und Δ hu = u S : d. Ein dem vorigen sehr ähnliches Instrument ist der Tachymetertheodolit mit Tangensablesung von Bell-Elliot [27]. – Das Prinzip des Kontakt- und Hebeldistanzmessers besteht darin, daß das Fernrohr für die Zielungen an zwei feste Punkte eines vertikalen Führungsstückes, oder daß statt des Fernrohrs ein mit ihm verbundener Hebel an zwei feste Punkte eines horizontalen Führungsstückes angeschlagen wird. Dann ist S proportional L. Nach Fig. 7 in Bd. 2, S. 785 ist S = L d : p = k L, wenn d : p = k; Δ h = S tg α. Nach diesem Prinzip sind konstruiert die Instrumente von Gentilli, Sanguet, Coradi und Löwe; s. Bd. 2, S. 786 und die da angegebene Literatur. Bei Sanguet wird tg α an einer Höhenskala abgelesen. Die übrigen Konstruktionen sehen Bestimmung des Höhenwinkels α an einem Höhenkreise oder Bogen vor. Hier ist ferner zu nennen das Universaltachymeter Láska-Rost. Die ganze Kontaktvorrichtung kann mit der Fernrohrkippung auf einer Horizontalschiene verschoben werden. Eine geringe Fernrohrkippung innerhalb der Kontakte wird mit einer Tangentenschraube vorgenommen. Durch zweimalige Ablesung vor und nach der geringen Fernrohrkippung erhält man Ls und daraus S = 100 Ls. Das anallaktische Fernrohr hat ein Okularmikrometer, dessen Kopf drehbar ist. Die Mikrometertrommel soll bei Höhenwinkeln oben, bei Tiefenwinkeln unten stehen. Der Höhenkreis hat zwei Trommelteilungen, eine Gradteilung und eine andre nach einer Funktion von α, ähnlich wie beim Tachymeter von Tichy und Starke. Die letzte Teilung gibt die Stellung des Okularmikrometers an, mit der der Lattenabschnitt Lh durch zweimalige Ablesung gewonnen wird. Dann ist Δ h = 100 Lh. Außerdem ist noch eine Berechnung von Δ h = S tg α möglich [28].
4. Selbsttätig reduzierende Tachymeter. Eine unmittelbare Reduktion der bei geneigter Ziellinie bestimmten schiefen Entfernung ist durch verschiedene Konstruktionen erstrebt worden, ohne daß diese bisher allgemein Anwendung gefunden haben. Es sei hingewiesen auf die[406] oben bereits erwähnte Vertikalkreisteilung beim Goulierschen Tachymeter, [13], S. 427, und auf andre eigenartige Einrichtungen der französischen Instrumente mit horizontalen und vertikalen Distanzfäden, die sogenannten Euthimeter, besonders auch auf die Latten, [13], S. 417. Ferner sind die italienischen Konstruktionen anzuführen. Bei dem reduzierenden Tachymeter von Porro mit sthenallaktischem Fernrohr soll die Reduktion durch Veränderung des Linsensystems erfolgen, die durch eine Gelenkvorrichtung mit der Kippung nach cos2 α ausgeführt wird. Dem gleichen Zwecke dienen die Anordnungen von Baggi [29] und von Reina [30], bei denen durch Gelenk- und Kurbelbewegungen der Fadenabstand nach cos2 α verändert wird. Die Reduktionstachymeter von Roncagli und Urbani haben hinter dem Diaphragma des anallaktischen Fernrohrs ein nach cos2 α geteiltes Glasmikrometer. Bei der älteren Konstruktion wurde das Mikrometer nach dem gemessenen Zenitwinkel mit einer Schraube eingestellt. Danach ergeben die Ablesungen an den Distanzmeßlinien den der horizontalen Entfernung entsprechenden Lattenabschnitt [31]. Dagegen ist an einem neueren Tachymeter von Roncagli eine aus Hebelarm und Exzenter bestehende Vorrichtung angebracht, die das Mikrometer bei der Fernrohrkippung selbsttätig verschiebt. Ein Entwurf von Hammer, der den italienischen Vorgängen folgt, steht eine selbsttätige Verschiebung des Diaphragmaplättchens vor, auf dem ein Netz von Kurven nach cos2 α für die Entfernungen und nach sin α cos α für die Höhenunterschiede konstruiert ist [32]. Ein Entwurf von Nasso gründet sich auf dem gleichen Prinzip. Durch Einfachheit der Handhabung zeichnet sich das selbstreduzierende Tachymeter Hammer-Fennel aus. Es scheint auch, daß dieses Instrument den Zweck, welchem es dienen soll, erfüllt. Es ist für die topographische Tachymetrie bestimmt und erfordert nur eine einzige Einstellung des Fernrohrs auf die Latte und zweimalige Lattenablesung ohne irgendwelche Ablesungen am Instrument. In jeder Stellung des anallaktischen Fernrohrs werden 1 : 100 der wagerechten Entfernung und 1 : 20 des Höhenunterschiedes an der lotrechten Latte mit einem Kurvendiagramm bestimmt, das in der linken Hälfte des Gesichtsfeldes erscheint. Eine Glasplatte mit dem Diagramm liegt über der Fernrohrkippachse. Das Bild des Diagramms wird durch zwei Prismen und eine Linse in der Bildebene des Objektivs entworfen, in der auch ein Horizontalfaden angebracht ist. Das Diagramm zeigt als Grundkurve einen 60° Zentriwinkel umfassenden Kreisbogen von 30 mm Halbmesser. Der Mittelpunkt muß in der Horizontalachse des Fernrohrs liegen. Ein Nullpunkt teilt die Grundkurve in zwei gleiche Stücke. Der Abstand der Entfernungskurve im Radius des Nullpunktes ist p = F : 100, wenn F die äquivalente Brennweite des Liniensystems bedeutet. Für andre Punkte ist der Abstand p' = p cos2 α. Die Höhenkurven für positive und negative Δ h gehen vom Nullpunkte des Grundkreises aus. Die Abstände der Kurvenpunkte sind bestimmt nach h' = 5 p' tg α [33].
5. Schiebe- oder Projektionstachymeter. Bei diesen Instrumenten ist eine andre Methode zur Ableitung der wagerechten Entfernungen angewendet. Fig. 5 zeigt ein Schiebetachymeter von Wagner-Fennel. Mit dem Fadendistanzmesser ist eine Schiebeskala A A' verbunden. Auf dieser Skala wird die schiefe Entfernung in verjüngtem Maßstabe mit dem Nonius b eingestellt. Darauf wird an der horizontalen Skala B B' die horizontale Entfernung mit dem Nonius c und an der vertikalen Skala die Höhe mit dem Nonius a abgelesen. Die letzte Skala kann mit der Schraube E derart verschoben werden, daß am Nonius d die Höhe der Kippachse über dem Vermessungshorizont eingestellt erscheint [34]. Ein ähnliches Instrument ist von Kreuter [35], ein älteres von Kiefer [36] konstruiert. Die Instrumente bedingen eine Lattenstellung rechtwinklig zur Ziellinie. Puller hat das Schiebetachymeter für vertikale Lattenstellung eingerichtet. Eine mit dem Fernrohr verbundene Stange steht rechtwinklig zur unteren Ziellinie des Fadendistanzmessers. Mit einem Schieber auf der Stange wird die schiefe Entfernung an einer Skala eingestellt, die gegen die Horizontale um den distanzmessenden Winkel nach unten geneigt ist. Im übrigen ist die Einrichtung ähnlich der des Wagnerschen Instruments [37]. Eine neuere Form des Instruments hat einen unbeweglichen Sektor mit einem Diagramm zur Einstellung eines Zeigers entsprechend dem Lattenabschnitte L [38]. Schließlich kann man zu dieser Art Instrumente auch noch Jähns Vielmesser rechnen [39]. Ueber Vergleiche zwischen Schiebe- und Kreistachymeter s. [15]. Im allgemeinen haben die Kreistachymeter eine größere Verbreitung gefunden.
6. Tachygraphometer. Jeder Meßtisch mit einer tachymetrischen Kippregel ist eigentlich ein Tachygraphometer (s. Bd. 6, S. 392). Anzuführen ist hier die tachymetrische Kippregel Patent Tichy-Starke [9], Die Einrichtung des Fernrohrs mit einem Okularmikrometer ist wegen verhältnismäßig unsicherer Aufstellung auf dem Meßtisch nicht zu empfehlen. Die Patentkippregel Láska-Rost ist wie das Tachymeter gleichen Namens nach dem unter 3. beschriebenen Prinzip konstruiert, jedoch richtigerweise ohne Okularmikrometer [41]. Bei der Tachymeterkippregel von Soldati ist der Höhenkreis durch einen Berechnungssektor ersetzt, auf dem die Horizontalentfernung und der Höhenunterschied mit Hilfe von[407] zwei Kurvenscharen ermittelt werden. – Tachygraphometer in engerem Sinne sind Instrumente besonderer Konstruktion. Ein Dreifuß trägt eine kreisförmige Scheibe von 30–45 cm Durchmesser, über deren Mitte sich eine Regel mit der Tachymetervorrichtung dreht. Auf der Scheibe wird das Meßtischblatt durch Halter befestigt. Für jeden Standpunkt ist ein Meßtischblatt erforderlich. Das Auftragen der Messungspunkte geschieht bei den Instrumenten mit Schiebetachymeter durch eine Pikiernadel, die sich mit dem Schieber einstellt, sonst aus Hand mit einer Nadel nach dem Maßstab der Regel. Häufig hat die Scheibe eine Gradteilung, die gestattet, das Instrument auch als Theodolit zu benutzen. Unter 3. ist bereits aufgeführt der Universaltacheograph Ziegler-Hager [24]. Mit den unter 5. beschriebenen Schiebetachymeteranordnungen sind versehen das Tachygraphometer Wagner-Fennel [34] und der Puller-Breithauptsche Schnellmesser [37]. Das Topometer Hammer-Fennel [43] ist ein Tachygraphometer mit selbsttätig reduzierendem Tachymeter. Dessen Beschreibung s. unter 4. Eine Verbindung von Theodolittachymeter und Meßtisch ist der Geländemesser von Koch [44].
7. Nivelliertachymeter sind Nivellierinstrumente, die mit einem Horizontalkreis oder einer Bussole sowie mit Distanzmeßvorrichtung ausgerüstet sind. Neben dem Fadendistanzmesser kommen auch die distanzmessenden Schrauben in Betracht (s. unter 3.).
Wegen der Distanzlatten s. Bd. 2, S. 782, und [1], S. 733. Ueber horizontale Lattenhaltung, die jedoch nur wenig angewendet wird, s. [13], [15], [2], S. 381 und 384, [21] in Bd. 2, S. 789; Geschichtliches s. [2].
II. Die tachymetrische Aufnahme.
1. Die Aufnahme im Felde. Der Gang der Bestimmung eines Geländepunktes mit dem berichtigten Theodolittachymeter mit Fadendistanzmesser ist:
a) Einstellung des Vertikalfadens auf die Lattenmitte.
b) Ablesung des Lattenabschnittes zwischen den Distanzfäden. Hierzu wird der untere oder obere Faden auf eine Marke (z.B. 1 m oder 2 m) eingestellt und am andern wird abgelesen, wobei die Mittelfadenablesung eine Probe gewährt, oder der Mittelfaden wird auf eine Marke (z.B. 2,0 m) eingestellt, und die Seitenfäden werden abgelesen, wobei die Ergänzung eine bequeme Probe gegen grobe Fehler gibt. Weitere Proben und Erhöhung der Genauigkeit erhält man durch entsprechende Verbindung dieser Ablesungen sowie durch Anwendung weiterer Fadenpaare wie bei den Clepscykeln [6].
c) Ablesung des Vertikalkreises. Ist der Mittelfaden auf eine Lattenmarke (z.B. 2,0 m) eingestellt worden, so kann bei einspielender Höhenkreislibelle sofort die Ablesung genommen werden, während bei Einstellung des unteren oder oberen Fadens auf eine Lattenmarke eine zweite Einstellung des Mittelfadens erforderlich wird, um die Veränderung der Zielhöhe h zu eliminieren. Häufig wird lz = i gemacht (s. Fig. 1).
d) Die Ablesung des Horizontalkreises, oder der Bussole. Die Ablesungen der beiden Kreise geschehen je nach der Beschaffenheit und Berichtigung des Instrumentes, den erforderlichen Proben u.s.w. an einem oder an beiden Zeigern. Auf Ablesung in beiden Fernrohrlagen wird bei Geländepunkten in der Regel verzichtet. Nach der zu b) notierten Distanzfadenablesung wird der Lattenträger abgerufen, einen andern Punkt aufzusuchen. Am Anfang und Schluß der Ablesungen für einen Standpunkt ist ein scharf bezeichneter Punkt (Kirchturm, Wetterfahne, trigonometrisches Signal) zur Prüfung der Instrumentstellung anzuzielen. Die Ablesungen werden in einem passend eingerichteten Feldbuch aufgeschrieben, worin gleichzeitig die ganze Berechnung ausgeführt wird.
Bei der Anwendung andrer Instrumente erleidet das Verfahren eine entsprechende Modifikation. Beim Meßtischtachymeter werden die gewonnenen Ergebnisse sofort eingetragen. Die topographische Abteilung der preußischen Landesaufnahme benutzt die tachymetrische Kippregel (Bd. 6, S. 393) und eine im Felde zu gebrauchende Tabelle [48].
2. Die Bestimmung der Tachymeterstandpunkte (Stationierung). Als Unterlage für jede tachymetrische Geländeaufnahme ist eine Anzahl passend verteilter, nach Lage und Höhe gegebener Festpunkte erforderlich. Die Auswahl hängt von Zweck und Ausdehnung der Aufnahme ab. Bei kleinen, in sich geschlossenen Aufnahmen genügt ein Rahmen von Dreiecken, in denen die Winkel und alle Seiten tachymetrisch doppelt gemessen sind. Für ausgedehnte Arbeiten ist der Anschluß an die Landestriangulation und die Einschaltung einer Anzahl Punkte, besonders durch Rückwärtseinschneiden, erforderlich (vgl. Triangulierung). Hierauf gründet[408] sich eine Polygonisierung, deren Punkte nach Lage (Koordinaten) und Höhe tachymetrisch, zuweilen aber auch in gewöhnlicher Weise (s. Bd. 7, S. 183) und durch Nivellierung (s. Bd. 6, S. 649) bestimmt werden. Dadurch ist ein durch Pfähle, Drainrohre oder Steine (Grenzsteine) bezeichnetes Festpunktsystem geschaffen, an das die eigentliche Geländeaufnahme angeschlossen wird. Sie geschieht durch kurze Aufnahmezüge zwischen den gegebenen Punkten oder durch Einzelaufnahme von den gegebenen Stationen aus. Hierbei können Zielungen bis zu einigen Hundert Metern genommen werden.
3. Der Tachymeterzug. Die Anordnung entspricht derjenigen des Polygonzuges (Bd. 7, S. 183) oder des Bussolenzuges (Bd. 2, S. 411), unter Hinzunahme der Distanz- und Höhenmessung. Die Entfernungen zwischen den Standpunkten werden doppelt bestimmt, wodurch eine ausreichende Genauigkeit zu erzielen ist (vgl. Bd. 2, S. 786). Zweckmäßig ist es, in die Strecke zwei Wechselpunkte einzuschalten und je zwei Teilstrecken von den beiden Endpunkten aus zu messen. Die Höhenbestimmung geschieht durch Uebertragung der Höhe der Festpunkte auf die Instrumentachse Hi = Hn + lz – Δ h (vgl. das Zahlenbeispiel) oder durch unmittelbare Messung der Standpunkthöhe i (vgl. Fig. 1) Hi = Hp + i. Die Messung zwischen den Stationen wird ausgeführt mit Hilfe von Wechselpunkten wie im Nivellierzuge (Bd. 6, S. 649); eine Sicherung bietet hierbei doppelte Anbindung. Im Tachymeterzuge sind grundsätzlich alle Ablesungen in zwei Fernrohrlagen und an zwei Zeigern zu nehmen. Ueber die Messung wird ähnlich wie bei der Stückvermessung (s.d.) ein Handriß geführt, in den die Nummern der Punkte in Uebereinstimmung mit dem Feldbuche eingetragen werden. Kleinaufnahmen werden auf Grund der tachymetrisch bestimmten Punkte durch Nebenmessungen mit Taschenbandmaß und Handbussolen ausgeführt. Es ist nötig, daß größere Aufnahmen durch zwei Techniker bewirkt werden, von denen einer die Arbeit leitet, den Handriß führt und die Lattenträger (mindestens zwei) anweist, während der andre mit einem Gehilfen das Instrument bedient. Weitere Anleitung und praktische Winke in [1], [2], [7], [8], [13], [45]–[47] sowie in zahlreichen Artikeln in den Fachzeitschriften, über welche eine Uebersicht in [49]; vgl. besonders [50].
III. Die Ausarbeitung.
Zur Ausrechnung der Entfernung und des Höhenunterschiedes nach den unter I. angeführten Formeln dienen verschiedene Hilfsmittel:
a) Tachymetertafeln, Tabellen, aus denen unmittelbar mit den Argumenten L und α (bezw. z) die gesuchten Werte S und Δ h entnommen werden können. Eine ausführliche Tafel dieser Art für die Produkte L cos2 α und 1/2L sin 2α gibt Jordan [51]. Aus dieser zunächst für k = 100 aufgeteilten Tabelle können für die weitaus meisten Fälle der Praxis die gesuchten Werte ohne weiteres entnommen werden, für k = 50 bezw. 200 ist L entsprechend zu halbieren bezw. zu verdoppeln. Weicht k von der runden Zahl ab, so macht eine leichte Umrechnung die Tafel brauchbar. Eine Zusammenstellung der Literatur über die wichtigsten Tachymetertafeln gibt [1], S. 765.
b) Der tachymetrische Rechenschieber ist ein logarithmischer Rechenschieber, bei dem die Logarithmen der obengenannten Funktionen auf Stab oder Zunge aufgetragen sind. Derartige Schieber sind in verschiedener Anordnung und Größe (25 cm und 50 cm) konstruiert worden von Wild, Porro, Moinot und Werner [7], [45], wodurch die Tachymeterrechnung wesentlich gefördert worden ist. Am besten ist die Anordnung, bei welcher eine Einstellung die Werte für S und Δ h liefert. Hierbei enthält der Stab oben und unten zwei identische Skalen der Logarithmen der Zahlenreihe 1, 2, 3 ..., die Zunge oben die Logarithmen der Funktion 1/2sin 2α, unten von cos2 α so angeordnet, daß unter Berücksichtigung der Konstanten k nach Einstellung des Zeigers der Zunge auf L in den Zahlenreihen des Stabes, an den Argumenten α der Zunge sofort S und Δ h am Stab abgelesen werden können. Ein logarithmischer Tachymeterschieber in Scheibenform ist von Miller in Innsbruck [52] konstruiert, vgl. a. [53]. Dechers Schieber. Logarithmische Tachymeterschieber liefern in Deutschland besonders Dennert & Pape in Altona, Nestler in Lahr i. B. und Kern in Aarau (mit Gebrauchsanweisung).
c) Tachymeterdiagramme. Für viele Zwecke reicht die Genauigkeit gezeichneter Diagramme aus, deren Benutzung sehr bequem ist. Zunächst kann der einfache Rechenquadrant mit Gradteilung und Quadratnetz (sinus-cosinus-Quadrant) benutzt werden, wozu für L cos2 α eine doppelte Eintragung nötig wird; S und Δ h können sofort abgelesen oder Δ h kann graphisch zu Hi addiert werden. Eine Reihe zweckmäßiger Strahlendiagramme mit entsprechender Ueberhöhung für die Höhenbestimmung gibt Jordan [1], S. 757, für die Funktionen L cos2 α und S tg α sowie 1/2 L sin 2 α. Dem gleichen Zweck dienen die Schichtentafeln (Isoplethentafeln) nach Vogler [54], das sind graphische Tafeln mit zwei Eingängen L und α, an deren Linienschar die gesuchten Werte S und Δ h abgelesen werden, und die graphischen Tafeln für Tachymetrie von Wenner [57 a]. Weitere Hilfsmittel sind die mechanischen Vorrichtungen, wie Teischingers Schiebebrett [55], der Reduktionsapparat von Piat [56], der Tachymeterquadrant von Pull er sowie der Tachymeterschieber von Puller [57]. Alle diese verschiedenen Hilfsmittel, die Tabellen und je nach der Einübung die mechanischen Mittel (Rechenschieber, Schieberdiagramme) sowie die Strahlendiagramme gewähren eine so bequeme und rasche Ableitung der Endresultate, daß die Versuche, durch mehr oder weniger komplizierte Projektionsapparate, welche zudem die Feldarbeit erschweren, diese einfachen Ermittlungen zu ersetzen, bisher ohne Erfolg geblieben sind.
Nach Berechnung der Feldbeobachtungen mit den obenerwähnten Hilfsmitteln (vgl. das Zahlenbeispiel) erfolgt die Anfertigung der Karte. Zuerst sind die gegebenen Punkte einzutragen, wozu bei umfangreichen Arbeiten mit trigonometrischem Anschluß und Koordinatenberechnung für die Hauptzüge (s. Polygonisierung, Bd. 7, S. 183) die Herstellung eines Quadratnetzes (s. Kartierung, Bd. 5, S. 394) erforderlich ist. Das Eintragen der Richtungen[409] und Entfernungen von den Stationspunkten aus erfolgt mit Hilfe eines Strahlenziehers (Transporteur, Rapporteur). Dieser wird auf dem in der Karte verzeichneten Standpunkt zentrisch aufgelegt und nach gegebenen Anschlußrichtungen orientiert; dann werden nach dem Feldbuche der Reihe nach alle Richtungen gezogen, die horizontalen Entfernungen abgesetzt und die Höhenzahlen beigeschrieben.
Für viele Zwecke sind die bekannten einfachen Transporteure aus Metall und Papier oder auch die auf Pauspapier gezeichneten Strahlenzieher mit 1° oder 1/2° Teilung ausreichend; für genauere Arbeiten ist eine Reihe von Auftragapparaten konstruiert worden; vgl. Alhidadentransporteur, Bd. 1, S. 133, sowie auch Schlesingers Tachygraph [58], Millers Auftragapparate u.a.; s. [1], S. 786. – Weiterhin erfolgt die Auszeichnung des Lageplanes und die Konstruktion der Horizontalkurven nach den hierfür geltenden Bestimmungen. Allgemeine Regeln s. Karte, Bd. 5, S. 385. Der Maßstab der Karte richtet sich nach dem Zweck der Aufnahme; für spezielle technische Zwecke (Vorarbeiten) wählt man 1 : 1000 bis 1 : 5000. – Bei der Benutzung von Tachygraphometern werden sämtliche Punkte sofort im Felde eingetragen.
IV. Höhenmessung bei vorhandenem Lagepläne.
Neben dem eben besprochenen vollständigen tachymetrischen Verfahren hat die tachymetrische Höhenmessung für sich eine Bedeutung, wenn bereits eine Karte, z.B. eine Katasterkarte, nach einer Lagemessung hergestellt wurde. Besonders in unebenem Gelände ist dann die tachymetrische Höhenmessung dem eigentlichen Nivellieren (Bd. 6, S. 642) in bezug auf Schnelligkeit und Billigkeit überlegen, da das Nivellierinstrument nur eine geringe Höhenzone (4–5 m) beherrscht.
Wird das Instrument auf einem in der Karte gegebenen oder bequem und sicher einzumessenden Punkte aufgestellt, so daß die Entfernungen S nach den Geländepunkten unmittelbar aus der Karte entnommen werden können, so braucht nur der Höhen- oder Zenitwinkel abgelesen zu werden, um nach Δ h = S tg α S ctg z sofort den Höhenunterschied oder die Höhe aus einem der obenerwähnten Diagramme entnehmen zu können. Hierbei genügt als Ziellatte eine einfache Latte mit Zielscheibe (lz = konstant oder = i); sollen auch solche Punkte, die in der Karte noch nicht dargestellt sind, bestimmt werden, so kann die Distanzmessung mit Distanzlatten zu Hilfe genommen werden, und das Verfahren wird dann zu einem kombinierten.
Für untergeordnete Arbeiten kann auch an Stelle des Tachymeters irgend ein Freihandinstrument (s. Bd. 4, S. 190, und Bd. 5, S. 91) benutzt werden, wobei dann die Entfernungen wie vorher aus der Karte entnommen oder aber mit einem Meßband in schiefer Lage gemessen werden; im letzteren Falle ist Δ h = S sin α. Diese Meßbandhöhenzüge sind besonders für Zwischenzüge in dichten Holz- oder auch für schwierige Querprofile sehr zweckmäßig; soll der Zug mit seinen Zwischenpunkten eingetragen werden, so werden die Streckenazimute mit einer Freihand- oder besser einer Stockbussole (auf dem Meßbandstab) gemessen. Die Berechnung und Austragung erfolgt am einfachsten graphisch oder mit Tabellen. Weiteres hierüber s. [59] und [1], S. 788. An Stelle der tachymetrischen Höhenmessung findet für generelle Bestimmungen auch die barometrische Höhenmessung mit Federbarometern (Bd. 3, S. 655) Anwendung; vgl. hierüber Bd. 5, S. 94.
V. Anwendung und Genauigkeit.
Die verschiedenen tachymetrischen Messungsmethoden finden bisher hauptsächlich Anwendung bei geometrischen Vorarbeiten. Es genügt hierfür, wenn man bei Zielungen bis zu einigen hundert Metern die gegenseitige Lage und Höhe der Punkte innerhalb einiger Dezimeter genau bestimmt hat. Dies ist durch die erwähnten einfachen Tachymeter, an deren Kreise einzelne Minuten abgelesen werden, bei guten Fernrohren und gut geteilten Zentimeterlatten erreichbar. Weiterhin wird von der Tachymetrie Gebrauch gemacht bei den unter besonderen Verhältnissen stattfindenden Vermessungen in den auswärtigen Kolonialgebieten sowie allgemein bei den topographischen Aufnahmen (1 : 25000) mit Meßtisch und Tachymeterkippregel. Hierbei sind die Anforderungen an die Genauigkeit erheblich geringer; für die Entfernungsbestimmung genügt eine in Dezimeter oder 1/2 dm (Distanzkonstante 1 : 200) geteilte Latte; auch können die Zielweiten erheblich größer (500 m und mehr) genommen werden. – Anderseits ist die Tachymetrie zur exakten Spezialaufnahme der Katastervermessungen bisher nur für vereinzelte Gebiete im Gebirge (vgl. z.B. [60]) zur Anwendung gekommen, obwohl schon bei der auf dem Meßtischverfahren gegründeten alten bayrischen Landesvermessung etwa 1813 die Distanzmessung mit Reichenbachschen Distanzmessern eingeführt worden ist. Während nun die Genauigkeit der einfachen Tachymetrie für die Katasteraufnahmen in schwierigem Gelände bei sorgfältigem Verfahren als hinreichend bezeichnet werden kann, haben anderseits die seit Porro [61] angestellten Versuche, mittels feinerer und leistungsfähigerer Apparate die Tachymetrie auch für exakte Spezialvermessungen auszubilden, zu ihrer allgemeineren Anwendung bisher nicht geführt. Dies hat seinen Grund darin, daß eine solche Feintachymetrie ebenso wie die Feinnivellierung (Bd. 6, S. 654) an kurze Zielweiten und beschränkte Arbeitszeit im Felde gebunden ist. Dadurch geht der in ihrer Einfachheit und Allgemeinanwendbarkeit gegründete Vorteil der Methode gegenüber der Linearmethode (s. Stückvermessung) verloren. Ferner ist die tachymetrische Polarkoordinatenmessung weder für eine exakte Fehlerausgleichung, wie sie in den Messungslinien der Stückvermessung (s.d.) möglich ist, noch für ein rationelles Fortführungsverfahren (s. Kataster, Bd. 5, S. 404) geeignet.
Literatur: Die tachymetrischen Instrumente und Aufnahmeverfahren sind behandelt in den bei Geodäsie unter [4]–[10] genannten Werken, besonders in [1], Jordan, Handbuch der Vermessungskunde, Bd. 2, fortgesetzt von Reinhertz, 7. Aufl., bearbeitet von Eggert, Stuttgart 1908. – Ferner s. [2], Eggert Einführung in die Geodäsie, Leipzig 1907. – Eine gute Uebersicht[410] über die Instrumente mit Literaturangaben findet sich in [3], Löschner, Oesterr. Zeitschr. f. Verm. 1907, S. 12 u. 106. – Einige Sonderschriften sind [4], Tinter, Zeitschr. f. Instr. 1882, S. 117, 157. – [5] Jordan, Tachymeter mit Zelluloidhöhenbogen, Zeitschr. f. Verm. 1896, S. 14. – [6] Salmoiraghi, Instrumenti e methodi moderni di geometria applicata, Mailand 1874, 1885, deutscher Auszug in Carls Repertorium 1876, S. 85. – [7] Werner, Die Tachymetrie und deren Anwendung bei Tracestudien, Wien 1873, 1885. – [8] Schell, Die Tachymetrie mit besonderer Berücksichtigung des Tachymeters von Tichy u. Starke, Wien 1880. – [9] Ders., Die Terrainaufnahme mit der tachymetrischen Kippregel von Tichy u. Starke, Wien 1881. – [10] Reinhertz, Zeitschr. f. Verm. 1902, S. 213; Fennel, ebend. 1902, S. 214. – [11] Ott, Zeitschr. f. Instr. 1893, S. 144. – [12] Deubel, Zeitschr. f. Verm. 1894, S. 193. – [13] Goulier, Études théorétiques et pratiques sur les levers topométriques et en particulier sur la tachéométrie, Paris 1892. – [14] Hensoldt, Zeitschr. f. Instr. 1885, S. 413. – [15] Hammer, Zeitschr. f. Verm. 1891, S. 195; Puller, ebend. 1893, S. 65; 1894, S. 10; Wagner, ebend. 1893, S. 540. – [16] Lorber, Zeitschr. f. Instr. 1886, S. 365. – [17] Puller, Zeitschr. f. Verm. 1895, S. 65. – [18] Friedrich, Das optische Distanzmessen, Wien 1881. – [19] Starke, Logarithmisch-tachymetrische Tafeln u.s.w., Wien 1885. – [20] Hogrewe, Praktische Anleitung zum Nivellieren u.s.w., Hannover 1800. – [21] Dörgens, Zentralblatt der Bauverwaltung 1893, S. 152. – [22] Decher, Neues Nivellierinstrument, München 1890. – [23] Klingatsch, Zeitschr. f. Verm. 1905, S. 337; Zeitschr. f. Instr. 1905, S. 305. – [24] Hammer, ebend. 1894, S. 242; v. Ziegler-Hager, Der Universaltacheograph, Luxemburg 1894. – [25] Vogler, Zeitschr. f. Verm. 1891, S. 145. – [26] Hammer, Zeitschr. f. Instr. 1895, S. 233. – [27] Ders., ebend. 1900, S. 282. – [28] Láska, ebend. 1905, S. 225, und Dokulil, Das Universaltachymeter Láska-Rost u.s.w., Wien 1906. – [29] Hammer, Zeitschr. f. Instr. 1896, S. 340. – [30] Ders., ebend. 1897, S. 287. – [31] Roncagli u. Urbani, ebend. 1893, S. 381; Roncagli, ebend. 1895, S. 180. – [32] Hammer, ebend. 1898, S. 241. – [33] Ders., Der Hammer-Fennelsche Tachymetertheodolit und die Tachymeterkippregel, Stuttgart 1901; Zeitschr. f. Verm. 1901, S. 153; 1903, S. 691; Zeitschr. f. Instr. 1900, S. 328; 1902, S. 21; Koppe, Zeitschr. f. Verm. 1902, S. 144. – [34] Fennel, Die Wagner-Fennelschen Tachymeter, Kassel 1886; Zeitschr. f. Verm. 1878, S. 57. – [35] Kreuter, Das neue Tacheometer, Brünn 1888. – [36] Puller, Zeitschr. f. Verm. 1896, S. 375. – [37] Ders., ebend. 1901, S. 531; Breithaupt & Sohn, Der Puller-Breithauptsche Schnellmesser, Selbstverlag, 1902; Hammer, Zeitschr. f. Instr. 1902, S. 160; Schoingt, Zeitschr. f. Verm. 1903, S. 408. – [38] Puller, ebend. 1903, S. 649. – [39] Jähns, Deutsche Bauztg. 1875, S. 92. – [40] Schell, Die Terrainaufnahme mit der tachymetrischen Kippregel, Wien 1881. – [41] Láska, Oesterr. Zeitschr. f. Verm. 1907, S. 35. – [42] Hammer, Zeitschr. f. Instr. 1902, S. 222. – [43] Ders., ebend. 1909, S. 129. – [44] Koch, Zeitschr. f. Verm. 1897, S. 33. – [45] Moinot, Lever de plans à la stadia, notes pratiques pour études de traces, 2e éd., Paris 1877. – [46] Orlandi, Tacheometria, corso pratico di topografia numerica, 2e éd., Turin 1896. – [47] Handbuch der Ingenieurarbeiten, herausgegeben von Heusinger v. Waldegg, Bd. 1, Leipzig 1880 (1883, 1898). – [48] Vorschrift für die Topographische Abteilung der Landesaufnahme, 2 Hefte, Berlin 1898. – [49] Zeitschr. f. Verm., Literaturberichte. – [50] Jordan, ebend. 1890, S. 401; Hammer, ebend. 1890, S. 641; 1891, S. 193, 241. – [51] Jordan, Hilfstafeln für Tachymetrie, 4. Aufl., Stuttgart 1908. – [52] Hammer, Zeitschr. f. Instr. 1893, S. 96. – [53] Decher, Rechenschieber zur Berechnung tachymetrischer Aufnahmen u.s.w., München 1882. – [54] Vogler, Anleitung zum Entwerfen graphischer Tafeln, Berlin 1877. – [55] Teischinger, Zeitschr. f. Instr. 1884, S. 92. – [56] Piat, Zeitschr. f. Verm. 1891, S. 25. – [57] Puller, ebend. 1893, S. 207; 1895, S. 389; 1896, S. 20; 1897, S. 363. – [57a] Wenner, ebend. 1905, S. 257. – [58] Pesek, ebend. 1878, S. 281. – [59] Jordan, ebend. 1876, S. 395; Hammer, ebend. 1896, S. 161; 1897, S. 202. – [60] Brönnimann, Die Katastervermessung auf Grundlage der in den schweizerischen Konkordatskantonen geltenden Vorschriften, Bern 1888. – [61] Porro, Sull' applicazione della Celerimensura alla formazione del gran libro fondiario italiano, Milano 1868.
(† Reinhertz) Hillmer.
Buchempfehlung
Anselm von Canterbury
Warum Gott Mensch geworden
Anselm vertritt die Satisfaktionslehre, nach der der Tod Jesu ein nötiges Opfer war, um Gottes Ehrverletzung durch den Sündenfall des Menschen zu sühnen. Nur Gott selbst war groß genug, das Opfer den menschlichen Sündenfall überwiegen zu lassen, daher musste Gott Mensch werden und sündenlos sterben.
86 Seiten, 5.80 Euro
Im Buch blättern
Ansehen bei Amazon
Buchempfehlung
Romantische Geschichten. Elf Erzählungen
Romantik! Das ist auch – aber eben nicht nur – eine Epoche. Wenn wir heute etwas romantisch finden oder nennen, schwingt darin die Sehnsucht und die Leidenschaft der jungen Autoren, die seit dem Ausklang des 18. Jahrhundert ihre Gefühlswelt gegen die von der Aufklärung geforderte Vernunft verteidigt haben. So sind vor 200 Jahren wundervolle Erzählungen entstanden. Sie handeln von der Suche nach einer verlorengegangenen Welt des Wunderbaren, sind melancholisch oder mythisch oder märchenhaft, jedenfalls aber romantisch - damals wie heute. Michael Holzinger hat für diese preiswerte Leseausgabe elf der schönsten romantischen Erzählungen ausgewählt.
- Ludwig Tieck Die beiden merkwürdigsten Tage aus Siegmunds Leben
- Karoline von Günderrode Geschichte eines Braminen
- Novalis Heinrich von Ofterdingen
- Friedrich Schlegel Lucinde
- Jean Paul Die wunderbare Gesellschaft in der Neujahrsnacht
- Adelbert von Chamisso Peter Schlemihls wundersame Geschichte
- E. T. A. Hoffmann Der Sandmann
- Clemens Brentano Die drei Nüsse
- Ludwig Achim von Arnim Der tolle Invalide auf dem Fort Ratonneau
- Wilhelm Hauff Jud Süss
- Joseph von Eichendorff Das Schloß Dürande
442 Seiten, 16.80 Euro
Ansehen bei Amazon
- ZenoServer 4.030.014
- Nutzungsbedingungen
- Datenschutzerklärung
- Impressum