Wellenbewegung
[511] Wellenbewegung (Undulation), die Fortpflanzung einer schwingenden Bewegung von Teilchen zu Teilchen, wobei jedes in der Fortpflanzungsrichtung folgende Teilchen seine Schwingung etwas später beginnt als das vorhergehende (Ausbreitung von Schwingungen). Ein anschauliches Bild von den Vorgängen bei der W. bietet ein wogendes Ährenfeld. Jede Ähre wird von dem Winde hinabgebogen, richtet sich aber vermöge der Elastizität des Halmes wieder empor, biegt sich wieder hinab etc. und vollführt in dieser Weise regelmäßig sich wiederholende Bewegungen oder Schwingungen. Die folgenden Ähren werden durch den Windstoß, der die erste zu schwingen zwang, um so später in Schwingungen versetzt, je weiter sie in der Reihe der Ähren von der ersten entfernt sind. Infolge der regelmäßigen Abwechselung von niedergebogenen und wieder ausgerichteten Ährenreihen zeigt die Oberfläche des Feldes in jedem Augenblick die Form von abwechselnden Vertiefungen und Erhöhungen; diese Wellenform sehen wir mit der Geschwindigkeit des Windes das Feld entlang eilen, während jede Ähre, an ihrem Orte festgewurzelt, ihre schwingende Bewegung macht. Wirst man einen Stein in ein ruhig stehendes Gewässer, so wird das an dieser Stelle hinabgedrückte Wasser durch den Druck des umgebenden Wassers wieder emporzusteigen genötigt, kommt aber, nachdem es den ursprünglichen Wasserspiegel erreicht hat, hier nicht plötzlich zur Ruhe, sondern setzt seine Bewegung nach auswärts fort, bis die entgegenwirkende Schwerkraft es wieder zum Herabsinken zwingt; so vollführt das durch den Stein zuerst aus seiner Ruhelage gebrachte Wasserteilchen eine Reihe auf- und abwärts gehender Schwingungen. Es kann aber das Gleichgewicht des Wasserspiegels nicht an einer Stelle gestört werden, ohne daß sich die Störung wegen der allseitigen Fortpflanzung des Wasserdruckes auch auf die ringsum benachbarten Wasserteilchen überträgt und diese veranlaßt, in gleichem Takte wie das zuerst gestörte Teilchen auf und ab zu schwingen, wobei jedes weiter entfernte Teilchen seine schwingende Bewegung etwas später beginnt als das ihm unmittelbar vorhergehende. Jede Hebung des zuerst gestörten Teilchens gibt zu einer Hebung der rings benachbarten Teilchen Anlaß, die, indem sie nach allen Richtungen fortschreitet, einen ringförmigen Wall um den Erregungsmittelpunkt bildet; die darauf folgende Senkung erzeugt ebenso eine kreisförmige Rinne, die als Wellental dem vorausgegangenen Wellenberg unmittelbar sich anschließt. Während also das zuerst erregte Teilchen eine ganze aus Hebung und Senkung bestehende Schwingung vollendet, erzeugt es eine vollständige aus Wellenberg und Wellental gebildete Welle, und indem es fortfährt zu schwingen, scheinen aus ihm immer neue Wellenringe hervorzuwachsen, die, sich erweiternd, mit gleichförmiger Geschwindigkeit nach außenhin fortschreiten. Es ist aber nur die Gestalt der Wasserfläche, die fortschreitet, nicht aber das Wasser selbst; die Wasserteilchen schwanken nur auf und ab, wie man an einem auf dem Wasser schwimmenden kleinen Holzstückchen, das diese schwingen de Bewegung mitmacht, leicht beobachten kann. Die Gesamtheit aller von demselben Erregungspunkte ausgehenden Wellenringe bildet ein Wellensystem. Jede vom Mittelpunkte des Wellensystems auf der wagerecht gedachten Wasserfläche gezogene Gerade heißt ein Wellenstrahl.
Alle Wasserteilchen, die im Ruhezustand auf dieser Geraden (A B, Fig. 1) lagen, befinden sich während der W. teils darüber, teils darunter, je nachdem sie augenblicklich einem Wellenberg oder einem Wellental angehören, und bilden daher in ihrer Aufeinanderfolge eine auf- und abgewundene Wellenlinie. Eine Strecke auf dem Strahl, die von einer vollständigen Welle, nämlich einem Wellenberg und einem Wellental, eingenommen wird, nennt man eine Wellenlänge. Betrachten wir die beiden Teilchen, die augenblicklich[511] die Gipfel zweier aufeinander folgender Wellenberge einnehmen, so finden wir beide gerade im Begriff, aus dieser ihrer höchsten Lage nach abwärts zu gehen; diese beiden Teilchen, die offenbar um eine ganze Wellenlänge voneinander abstehen, befinden sich also in dem nämlichen Schwingungszustand. Dasselbe gilt überhaupt von je zwei Teilchen, die um eine oder mehrere ganze Wellenlängen voneinander entfernt sind, ihre Bewegungen erfolgen in völliger Übereinstimmung. Nehmen wir dagegen zwei Teilchen, die um eine halbe Wellenlänge voneinander abstehen, von denen z. B. das eine auf dem Gipfel eines Wellenberges, das andre in der Tiefe des benachbarten Wellentales liegt, so sind dieselben in gerade entgegengesetzten Schwingungszuständen. Während nämlich jenes aus seiner höchsten Lage nach abwärts zu gehen beginnt, ist dieses im Begriff, aus seiner tiefsten Lage nach aufwärts zu gehen. Überhaupt sieht man ein, daß die Bewegungen zweier Teilchen, deren Abstand voneinander eine halbe Wellenlänge oder ein ungerades Vielfaches einer halben Wellenlänge beträgt, zueinander in vollkommenem Gegensatz stehen.
Wirst man zwei Steine in einiger Entfernung voneinander in ruhiges Wasser, so entstehen zwei Wellensysteme, die bei ihrer weitern Ausbreitung sich durchkreuzen; wo dies geschieht, sehen wir die Oberfläche von einem zierlichen Netzwerk kleiner Erhöhungen und Vertiefungen bedeckt, die durch das Zusammenwirken oder durch die Interferenz der beiden Wellensysteme entstehen. An allen Stellen nämlich, wo zwei Wellenberge zusammentreffen, erhebt sich das Wasser zu doppelter Höhe, und wo zwei Wellentäler sich durchkreuzen, senkt es sich zu doppelter Tiefe. An allen Stellen dagegen, wo ein Wellenberg mit einem Wellental zusammentrifft, wird das Wasser auf seine ursprüngliche Höhe, die es im Ruhezustand einnimmt, zurückgeführt, d. h. hier heben sich die beiden Wellenbewegungen gegenseitig auf. Überhaupt erleidet in einem Mittel, das von zweien oder beliebig vielen, gleichen oder ungleichen Wellensystemen bewegt wird, jedes Teilchen eine Verschiebung, welche die Summe ist aus allen ihm durch die einzelnen Wellensysteme in dem nämlichen Augenblick mitgeteilten Verschiebungen. Um diese Summe zu bilden, muß man alle Hebungen zusammenzählen, alle Senkungen abziehen; die wirklich stattfindende Bewegung des Teilchens ist sozusagen die Bilanz aus allen auf dasselbe einwirkenden Teilbewegungen. Man nennt diesen Satz das Prinzip der Übereinanderlagerung (Superposition) der Schwingungen, weil er in der Tat nichts andres aussagt, als daß jedes Wellensystem sich genau so über eine bereits von Wellen bewegte Oberfläche legt, wie es sich, wenn es allein vorhanden wäre, über die ruhende Oberfläche gelegt haben würde. Jedes Wellensystem bildet sich aus und behauptet sein besonderes Dasein im Durcheinanderwogen mit den andern und schreitet, nachdem es diese durchkreuzt und mit ihnen zusammengewirkt (interferiert) hat, auf der noch ruhigen Wasserfläche weiter, als ob es nie eine Störung erlitten hätte.
Dies gilt auch für Wellen verschiedener Länge, wobei neue, oft sehr komplizierte Wellenformen infolge der Superposition entstehen. Umgekehrt kann man nach Fouriers Satz auch die komplizierteste Wellenform als Aggregat einfacher Sinuswellen, wie Fig. 1, auffassen, deren Teilchen Abstände von der Mittellinie haben, die dem Sinus des Lichtstrahlwinkels eines gleichmäßig im Kreise umlaufenden Punktes entsprechen, woher der Name. (Bei elektrischen Wechselströmen, die wegen Übereinstimmung der graphischen Darstellung mit mechanischen Schwingungen in Analogie gebracht werden können, wird die Wellenform häufig Stromwelle genannt.)
Während eine fortschreitende W. sich durch irgendein Mittel fortpflanzt, ahmt jedes Teilchen die schwingende Bewegung des ursprünglich erregten Teilchens nach. Da nun jedes Teilchen zu den ihm benachbarten in derselben Beziehung steht wie das erste Teilchen zu seinen Nachbarteilchen, so muß es auf seine Umgebung genau die nämliche Wirkung hervorbringen wie das zuerst erregte, also ebensogut wie dieses der Ausgangspunkt eines Wellensystems sein. Die unzählig vielen, gleichzeitig vorhandenen Teilwellensysteme (Elementarwellen), die von sämtlichen in Bewegung befindlichen Teilchen ausgehen, bringen aber durch ihr Zusammenwirken (ihre Übereinanderlagerung) genau das Hauptwellensystem hervor, das, rings um den Erregungsmittelpunkt sich ausbreitend, tatsächlich vorhanden ist. Dieser wichtige Satz (Huygenssches Prinzip) enthüllt den wahren Vorgang bei der Fortpflanzung der Wellen in einem allseitig ausgebreiteten Mittel, indem er den gegenseitigen Wirkungen der Teilchen, die rings um jedes Teilchen in gleicher Weise stattfinden, gebührende Rechnung trägt. In einem solchen Mittel kann eine Fortpflanzung der schwingenden Bewegung längs einer einzigen geraden Linie offenbar nicht stattfinden; immer wird es sich um die Fortpflanzung einer Welle oder eines Wellenstückes handeln. Zu jedem Wellenstück aber, wie klein man sich dasselbe auch vorstellen mag, gehören unzählig viele Strahlen, die zusammen ein Strahlenbündel ausmachen. In der Natur kommen niemals vereinzelte Strahlen, sondern nur Strahlenbündel vor. Da in einem nach allen Richtungen gleich beschaffenen Mittel die Wellen, z. B. die Schallwellen in der Luft, sich um den Erregungsmittelpunkt als Kugelschalen ausbreiten, so steht jeder Strahl als Kugelhalbmesser auf dem zugehörigen Wellenstückchen senkrecht. Denkt man sich dieses Wellenstückchen sehr klein oder sehr weit vom Erregungspunkt entfernt, so können die auf ihm senkrechten Strahlen als unter sich parallel und das Wellenstückchen selbst als eine ebene Fläche betrachtet werden. Überhaupt gehört zu einem Bündel paralleler Strahlen stets eine ebene Welle, die zur Richtung der Strahlen senkrecht steht.
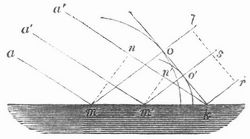
Sehen wir nun zu, was geschieht, wenn ein Bündel paralleler Strahlen a m a' k auf eine ebene Wand m k, z. B. auf die ebene Trennungsfläche zweier verschiedenartiger Mittel, trifft (Fig. 2). Indem die zu dem Strahlenbündel gehörige ebene Welle m n gegen die Wand fortschreitet, setzt sie nach und nach die an der Wand liegenden Teilchen m, m', k in schwingende Bewegung, und jedes derselben entsendet (dem Huygensschen Prinzip gemäß) sein eignes Wellensystem in das erste Mittel zurück. In dem Augenblick, in dem der Punkt k der Fläche von der einfallenden Welle erreicht wird, hat der zuerst getroffene Punkt m eine kreis- oder kugelförmige Teilwelle hervorgerufen, die sich rings um m ebenso weit ausgebreitet hat, als die Hauptwelle mittlerweile fortgeschritten ist, deren [512] Halbmesser m o sonach gleich der Strecke n k ist. Die zwischen m und k gelegenen Punkte haben inzwischen ebenfalls Teilwellen (Elementarwellen) erzeugt, deren Halbmesser um so kleiner sind, je näher sie dem augenblicklich noch in Ruhe befindlichen Punkte k liegen, der Punkt m' z. B. eine Welle, deren Halbmesser m'o' gleich k n' ist. Die gemeinschaftliche Berührungslinie k o sämtlicher Teilwellen, an der alle Bewegungen mit gleichen Schwingungszuständen eintreffen, stellt nun wieder eine Hauptwelle dar, die von der Trennungsfläche in das erste Mittel zurückgeht oder, wie man sagt. an dieser Fläche zurückgeworfen wurde (Reflexion). Wie man sieht, ist die zurückgeworfene Welle k o gegen die zurückwerfende Fläche m k unter dem nämlichen Winkel geneigt wie die einfallende. Das zugehörige zurückgeworfene Strahlenbündel m l k r, dessen Strahlen m l, m' s, k r zu der Welle k o senkrecht stehen, bildet mithin ebenfalls mit der Fläche m k und folglich auch mit einer auf ihr errichteten Senkrecht en, dem Einfallslot, den nämlichen Winkel wie das ein fallende Strahlenbündel.
Von den durch die ankommende Welle erschütterten Punkten der Trennungsfläche aus müssen aber auch Wellen in dem zweiten Mittel erregt werden, die sich jedoch mit einer andern Geschwindigkeit fortpflanzen als im ersten Mittel.
Die von dem Punkt a (Fig. 3), der von der auf M N einfallenden Welle a b zuerst getroffen wird, ausgehende Teilwelle wird daher in dem Augenblick, in welchem die einfallende Welle den Punkt b' erreicht, einen Halbmesser a e besitzen, der zu der gleichzeitig im ersten Mittel zurückgelegten Strecke b b' in demselben Verhältnis steht wie die Fortpflanzungsgeschwindigkeit im zweiten zu derjenigen im eriten Mittel. Da die von b' aus an diese erste Teil welle gezogene Berührungslinie b' c auch alle übrigen bis jetzt gebildeten Teilwellen berührt und sonach ihre Bewegungen zusammenfaßt, so stellt sie die ins zweite Mittel eindringende Hauptwelle vor. Wie mon sieht, hat die Welle beim Übertritt in das andre Mittel eine Schwenkung gemacht; ihre Front rückt in andrer Richtung vor als diejenige der einfallenden Welle a b. Das zu ihr gehörige Strahlenbündel a E b' F bildet daher mit dem Einfallot l a l' einen andern Winkel als das einfallende Strahlenbündel A a B b', es hat, wie man sagt. eine Brechung erlitten. Wenn, wie in der Figur, die Fortpflanzungsgeschwindigkeit im zweiten Mittel kleiner ist als im ersten. so ist der Brechungswinkel r kleiner als der Einfallswinkel i, das Strahlenbündel wird durch die Brechung dem Lot genähert oder zum Lot gebrochen. Das Verhältnis der Fortpflanzungsgeschwindigkeiten im ersten und zweiten Mittel, d. h. das Verhältnis der Strecken b b' und a e, heißt der Brechungsindex, auch Brechungsquotient, weniger passend Brechungsexponent. Unter Umständen werden die Wellen. die in das zweite Medium eindringen. nicht durchgelassen, sondern absorbiert, indem z. B. durch Reibung die Bewegung in Wärme umgesetzt wird. Befindet sich eine solche undurchlässige Schicht zwischen zwei durchlässigen Medien, die an einer Stelle durch eine Öffnung in der Schicht miteinander in Verbindung stehen, so dringt dort, entsprechend der geradlinigen Ausbreitung der Wellen, ein Strahl aus dem ersten Medium in das andre, begrenzt von den die Ränder der Öffnung streifenden Fortpflanzungsrichtungen, indes nicht mit völliger Schärfe. Es zeigt sich vielmehr auch außerhalb dieses Strahles eine, wenn auch mit größerm Abstand, immer schwächer werdende W., außerhalb des Strahles entsprechend einer Beugung der Fortpflanzungsrichtungen um die Ränder der Öffnung (Beugung der Wellen, s. Beugung des Lichtes und Elektrische Wellen).
Bei einer W. können im allgemeinen die Schwingungen der einzelnen Teilchen des in W. befindlichen Stoffes sowohl in der Richtung, nach der die Welle fortschreitet, d. h. in der Richtung des Strahles, erfolgen (longitudinale oder Längsschwingungen), als auch senkrecht zur Fortpflanzungsrichtung vor sich gehen (transversale oder Querschwingungen). Transversalwellen sind nur möglich in Körpern, die Verschiebungselastizität besitzen, d. h. in festen Körpern; in Flüssigkeiten und Gasen können sich also nur Longitudinalwellen (s. Schall) fortpflanzen, d. h. Wellen, die aus einer regelmäßigen Aufeinanderfolge von Verdichtungen und Verdünnungen bestehen. Die Entstehung solcher kann man sich z. B. bei einer schwingenden Stimmgabel klar machen.
Wird eine Stimmgabel angeschlagen, so nimmt sie, indem sich ihre Zinken nach innen biegen, die in Fig. 4 punktiert angedeutete Gestalt a'b' an, kehrt wieder in die Gleichgewichtslage a b zurück, überschreitet dieselbe, biegt nun ihre Zinken nach auswärts (a'' b''), kehrt wieder zurück u. s. f.; jede Zinke schwingt so zwischen zwei äußersten Lagen (a' und a'') nach denselben Gesetzen wie ein Pendel hin und her. Die schwingende Zinke veranlaßt die ihr zunächst liegenden Luftteilchen, diese Bewegung nachzuahmen; diese wirken ebenso auf die nächstfolgenden, und nach und nach wird eine ganze Reihe von Luftteilchen von der schwingenden Bewegung ergriffen. In Fig. 5 mögen die Punkte 1–12 die Ruhelagen von zwölf gleichweit abstehenden Luftschichten andeuten. Wir betrachten dieselben in dem Augenblick, in dem die Stimmgabelzinke a, nachdem sie zuerst von der Gleichgewichtslage nach einwärts, dann nach auswärts und wieder zurück in die Gleichgewichtslage sich bewegt hat, gerade im Begriff ist, wieder nach einwärts zu schwingen. Die Stimmgabel hat alsdann eine ganze Schwingung vollendet, um nun eine zweite zu beginnen. Hat sich während der Dauer dieser Schwingung die Bewegung bis zu der Luftschicht 12 fortgepflanzt, so ist diese gerade im Begriff, ihre erste Schwingung anzutreten, d. h. sie ist um eine ganze Schwingung hinter der Bewegung der Stimmgabel zurück. Die Luftschicht 1 ist alsdann, weil ihr Abstand von der Stimmgabel nur 1/12 ist, auch nur um 1/12 Schwingung gegen die Stimmgabel zurückgeblieben; sie hat demnach 11/12 einer ganzen [513] Schwingung vollendet, ist in ihre Ruhelage noch nicht zurückgekehrt, sondern befindet sich noch rechts von derselben. Ebenso haben die Luftschichten 2, 3, 4... resp. nur 10/12, 9/12, 8/12... ihrer Schwingung ausgeführt und befinden sich sonach im betrachteten Augenblick in den Stellungen, die in der Zeichnung angegeben sind; die Luftschicht 6 z. B. hat erst 6/12 oder 1/2 Schwingung ausgeführt, nämlich von ihrer Ruhelage nach einwärts und wieder in die Ruhelage zurück, und passiert also gegenwärtig ihre Ruhelage. Überblicken wir jetzt sämtliche gleichzeitige Stellungen der Luftschichten, so ergibt sich, daß die Schichten zu beiden Seiten von 6, nämlich zwischen 3 und 9, näher zusammengerückt sind, als es im Ruhezustande der Fall war, die Schichten von a bis 3 und von 9–12 aber weiter voneinander abstehen. Zwischen 3 und 9 ist demnach die Luft verdichtet, und in 6 findet das Maximum der Verdichtung statt; von a bis 3 und von 9 bis 12 ist die Luft verdünnt, und zwar befinden sich die Schichten bei a und bei 12 im Zustande der größten Verdünnung. Schwingt nun die Stimmgabel z. B. um 1/12-Schwingung weiter, so setzt auch jede Luftschicht ihre Bewegung um 1/12 Schwingung fort; die Luftschicht 7 z. B. erreicht jetzt ihre Ruhelage, und die Schichten 6 und 8 nehmen in bezug auf sie dieselben Stellungen ein, die 5 und 7 vorhin in bezug auf 6 innehatten; die größte Verdichtung rückt daher von 6 nach 7 und ebenso die stärkste Verdünnung von a nach 1 und von 12 nach 13 u. s. s. Während also jedes Luftteilchen, ohne sich weit von seiner Gleichgewichtslage zu entfernen, in engen Grenzen hin und her schwingt, pflanzen sich Verdichtungen und Verdünnungen durch die Reihe der Luftteilchen fort, wie Wellenberge und Wellentäler über eine Wasserfläche hineilen, ohne die bloß auf und ab schwankenden Wasserteilchen mit sich fortzuführen. Eine Verdichtung und die darauf folgende Verdünnung bilden zusammen eine ganze Welle; der Abstand (a bis 12) von einer Verdünnung bis zur nächsten oder von einer Verdichtung bis zur nächsten heißt die Wellenlänge. Die Wellenlänge ist demnach diejenige Strecke, auf die sich die schwingende Bewegung während der Dauer einer ganzen Schwingung fortpflanzt. Bezeichnet man die Wellenlänge mit λ, die Fortpflanzungsgeschwindigkeit mit v und die Schwingungsdauer mit t, so ist hiernach λ = v t. Jede ganze Schwingung des vibrierenden Körpers erzeugt eine ganze Welle; ist daher n seine Schwingungszahl, d. h. macht er n Schwingungen in einer Sekunde, so erzeugt er auch n Wellen, die zusammen eine Strecke einnehmen gleich derjenigen (v), auf die sich die Bewegung während einer Sekunde fortpflanzt, d. h. es ist nλ = v. Von einem schwingenden Punkt aus pflanzt sich der Schall durch Luft von gleichmäßiger Beschaffenheit in konzentrischen Kugelschalen fort, die sich abwechselnd im Zustande der Verdichtung und der Verdünnung befinden; jeder Radius einer solchen kugelförmigen Welle heißt ein Strahl. Die Reihe von Luftteilchen, deren Bewegung wir vorhin betrachteten, bildet einen solchen Strahl. Da die innerhalb einer Kugelwelle bewegte Luftmasse im quadratischen Verhältnis ihres Radius wächst und sich demnach die von der Schallquelle ausgehende Bewegungsenergie auf immer größere Luftmassen verteilt, so muß die Stärke der W. mit wachsender Entfernung abnehmen, und zwar steht sie im umgekehrten Verhältnis des Quadrats der Entfernung.
Querschwingungen beobachtet man z. B. an einem langen, zwischen den Punkten A und B (Fig. 1) ausgespannten Seil, wenn man demselben etwa in lotrechter Richtung einen Schlag versetzt; man sieht alsdann das Seil entlang Wellen sich fortpflanzen, wobei jeder Punkt des Seiles senkrecht zur Fortpflanzungsrichtung auf und ab schwingt. Ein von B nach A das Seil entlang blickender Beobachter würde die Schwingungen in einer lotrechten Richtung wie Fig. 3 B erfolgen sehen und an dem schwingenden Seil die obere und untere Seite, nach denen die Schwingungen abwechselnd gerichtet sind, von der rechten und linken Seite, nach welchen hin keine Schwingungen vor sich gehen, wesentlich verschieden finden. Er würde sich ferner überzeugen können, daß, wenn man das Seil durch einen Schlitz hindurchgehen läßt, die lotrechten Schwingungen sich ungehindert fortpflanzen, sobald man den Schlitz lotrecht stellt, sich dagegen nicht durch den Schlitz (auch Analysator genannt) fortpflanzen können, wenn man ihn wagerecht stellt. Da sich sonach der betrachtete Seilwellenstrahl A B nach verschiedenen Seiten verschieden verhält (ähnlich wie ein durch eine Turmalinplatte gegangener Lichtstrahl), so nennt man ihn »polarisiert«. Die Ebene, in der die Schwingungen stattfinden, heißt Schwingungsebene, die dazu senkrechte Ebene Polarisationsebene. Erteilt man dem Seil gleichzeitig mehrere Schwingungszustände in verschiedenen Ebenen, so gehen durch den Schlitz nur diejenigen Komponenten derselben hindurch, deren Schwingungsebene parallel zum Schlitz ist; der Schlitz wirkt, wie man sagt, als Polarisator.
Stehende Wellen bilden sich durch Interferenz zweier Wellen von gleicher Wellenlänge und Schwingungsweite, die sich in entgegengesetzter Richtung fortpflanzen. Tritt z. B. eine Longitudinalwellenbewegung in Luft (Schall) in eine am untern Ende verschlossene Röhre ein, so wird sie an diesem Ende der Röhre zurückgeworfen; durch das Zusammenwirken (Interferenz) der zurückgeworfenen mit den neu einfallenden Wellen wird in der Röhre ein eigentümlicher Schwingungszustand hervorgerufen, dessen einzelne Phasen durch Fig. 6, in der die Verdichtungen durch Wellenberge, die Verdünnungen durch Wellentäler versinnlicht sind, erläutert werden sollen; die schwach gezogene Wellenlinie stellt die einfallende, die punktierte die zurückgeworfene und die stark gezogene die aus dem Zusammenwirken beider entstandene Welle vor. Fig. 6 A bezieht sich auf den Augenblick, in dem die zweite ein fallende Welle, von a ausgehend, bis zum Boden e der Röhre vorgedrungen und die erste reflektierte Welle von e bis a zurückgekehrt ist. In diesem Augenblick fallen die Verdichtungen der einfallenden mit den Verdünnungen der zurückgeworfenen Welle und umgekehrt zusammen und heben sich gegenseitig vollkommen auf, alle Luftteilchen befinden sich in ihrer Gleichgewichtslage und besitzen ihre größte [514] Geschwindigkeit; nach einer Viertelschwingungsdauer (Fig. 6 B) ist die Verdichtung der einfallenden Welle von d nach e, die Verdünnung der zurückgeworfenen von d nach c gerückt, und eine neue zurückgeworfene Verdichtung bei e ist ihr gefolgt; es fallen also jetzt die Verdichtungen mit Verdichtungen, die Verdünnungen mit Verdünnungen zusammen und verstärken sich gegenseitig; wir haben nun, während jedes Luftteilchen seine äußerste Lage erreicht hat und momentan in Ruhe ist, bei e starke Verdichtung, bei c starke Verdünnung, in b und d dagegen weder Verdichtung noch Verdünnung; nach einer weitern Viertelschwingung heben sich Verdichtungen und Verdünnungen wieder auf (Fig. 6 C), und die Luftteilchen gehen durch ihre Gleichgewichts lagen mit ihrer größten Geschwindigkeit; nach dem letzten Viertel der Schwingungsdauer endlich (Fig. 6 D) findet bei e die stärkste Verdünnung und bei c die stärkste Verdichtung statt, während die Punkte b und d weder Verdichtung noch Verdünnung zeigen. In den Punkten b und d findet also während der ganzen Bewegung niemals Verdichtung und Verdünnung, wohl aber die lebhafteste Hin- und Herbewegung der Luftschichten statt; die bei c und d gelegenen Luftschichten dagegen bleiben selbst fortwährend in Ruhe, werden aber, indem die benachbarten Luftschichten entweder gleichzeitig gegen sie hin- oder von ihnen wegschwingen, abwechselnd verdichtet und verdünnt. Bei ihrem Gegenlauf bleiben also die beiden Wellen stets symmetrisch zu den Durchschnittspunkten ihrer Wellenlinien; an diesen Stellen, die je um eine halbe Wellenlänge voneinander abstehen, sind die Verschiebungen, die jede Welle hervorbringt, immer einander gleich und gleichgerichtet und summieren sich; in diesen Punkten, die man Bäuche nennt, sind daher die Teilchen in lebhaft schwingender Bewegung. Dagegen in den Punkten, die zwischen den Bauchstellen gerade in der Mitte liegen, also ebenfalls unter sich je um eine halbe und von den Bäuchen je um eine Viertel-Wellenlänge abstehen, sind die Verschiebungen immer gleich und entgegengesetzt; diese Punkte, die Knoten heißen, bleiben stets ruhig in ihrer Gleichgewichtslage. Die resultierende Bewegung bildet sich also derart aus, daß alle Teilchen gleichzeitig durch ihre Gleichgewichtslagen hindurchgehen und gleichzeitig nach ein Viertel-Schwingungsdauer ihre größten Ausweichungen erreichen, während die Knotenpunkte fest liegen bleiben. Die Form der Welle schreitet somit nicht fort, weshalb man solche Wellen »stehende« nennt im Gegensatze zu den bisher betrachteten »fortschreitenden« Wellen, bei denen jedes folgende Teilchen später als das vorhergehende durch die Gleichgewichtslage geht. Eine in stehende W. versetzte Luftmasse wird dadurch zu einem selbsttönenden Körper. Die Punkte e, c, a,..., in denen die stärkste Verdünnung und Verdichtung, aber keine Bewegung stattfindet, die sogen. Knoten, sind 0, 1/2, 2/2, 2/3, 4/2 u. s. f. Wellenlängen vom Boden der Röhre entfernt. Die Punkte d, b..., in denen niemals Verdichtung oder Verdünnung, aber die lebhafteste Hin- und Herbewegung stattfindet, sind die sogen. Bäuche; ihre Entfernung vom Boden der Röhre beträgt 1/4, 3/4, 5/4, 7/4... Wellenlängen. Da das offene Ende der Röhre mit der äußern Luft in Verbindung steht, so kann hier weder Verdichtung noch Verdünnung statthaben; es muß sich da selbst notwendig ein Bauch bilden. Soll daher die in einer Röhre enthaltene Luft durch einen schwingenden Körper zum Mitklingen gebracht, d. h. in stehende W. versetzt werden, so muß ihre Länge 1/4 oder 3/4 oder 3/411. s. s. von der Wellenlänge des erregenden Tones betragen. Ein und dieselbe Röhre wird ansprechen auf diejenigen Töne, deren Viertelwelle einmal oder dreimal oder fünfmal u. s. s. in ihrer Länge enthalten ist, deren Schwingungszahlen sich demnach verhalten wie die ungeraden Zahlen 1, 3, 5, 7...; der tiefste derselben heißt die Grundschwingung der Röhre, die folgenden die Oberschwingungen. Auch in einer beiderseits offenen Röhre kann die Luft in stehende W. versetzt werden; hier müssen an beiden Enden Bäuche entstehen; die Länge der Röhre beträgt daher 1/2 oder 2/3 oder 3/4 u. s. s. von der Wellenlänge des anregenden Tones, und die Schwingungszahlen der Tonreihe, deren sie fähig ist, verhalten sich wie 1, 2, 3, 4, 5... Die Grundschwingung einer offenen Röhre ist die Oktave der Grundschwingung einer gleich langen geschlossenen; damit eine offene Röhre dieselbe Grundschwingung gebe wie eine geschlossene, muß sie demnach doppelt so lang sein als diese. Auch Flüssigkeitssäulen und Stäbe aus festem Material können nach denselben Gesetzen wie Luftsäulen in stehende Längsschwingungen versetzt werden. Ein Metallstab z. B. wird in dieser Weise zum Tönen gebracht, wenn man ihn in seiner Mitte oder am einen Ende festhält und am andern Ende mit beharzten Fingern der Länge nach streicht; im ersten Falle verhält er sich wie eine offene, im letztern wie eine gedeckte Pfeife, indem seine einzelnen Querschichten in der Richtung der Längenachse des Stabes hin und her schwingen und an der festgehaltenen Stelle abwechselnd Verdichtung und Verdünnung hervorrufen. Auch kann man ganz in derselben Weise wie bei den Pfeifen aus der Schwingungszahl des Tones und der Länge des Stabes die Schallgeschwindigkeit in der Substanz, aus welcher der Stab besteht, berechnen. Es ergibt sich z. B., daß sich der Schall in Silber 9-, in Kupfer 12-, in Eisen 162/3-, in Tannenholz 18mal so schnell fortpflanzt als in Luft. Stehende Transversalschwingungen lassen sich z. B. bei einem gespannten Seil, dessen eines Ende man rasch in regelmäßigem Takt auf und a b bewegt (Seilwellen), am besten aber bei Saiten beobachten.
Saiten sind fadenförmige Körper, die, wenn man sie durch Zupfen oder Streichen mit dem Violinbogen aus ihrer durch Spannung hervorgerufenen geradlinigen Gleichgewichtslage bringt, in stehende Quer- oder Transversalschwingungen geraten, indem ihre Teilchen in zur Längsrichtung der Saite senkrechten Bahnen gleichzeitig hin und her schwingen (Fig. 7).
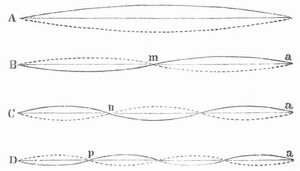
Um die Schwingungsgesetze der Saiten zu studieren, bedient man sich des Monochords (Fig. 8, S. 516), eines Resonanzkastens, auf dem zwischen den beiden Stegen a und b die Saiten entweder mittels des Stimmstocks s oder durch Gewicht P ausgespannt werden. Es ergibt sich in Übereinstimmung mit der Theorie, daß die Schwingungszahl einer Saite ihrer [515] Länge, Dicke und der Quadratwurzel aus dem spezifischen Gewicht umgekehrt, der Quadratwurzel aus der Spannung aber direkt proportional ist. Schwingt die Saite als Ganzes (Fig. 7 A), so gibt sie ihren Grundton; sie kann sich aber auch durch ruhende Punkte (Schwingungsknoten) in 2,3,4... schwingende Teile (Bäuche) zerlegen und gibt alsdann die zum Grundton harmonischen Obertöne, deren Schwingungszahlen 2, 3, 4... mal so groß sind als diejenigen des Grundtons.
Um die Schwingungsformen B, C, D hervorzurufen, berührt man die Saite bei m, n, p mit einem Pinsel oder setzt daselbst einen Steg unter und streicht bei a. Die Schwingungsknoten können sichtbar gemacht werden, indem man an den Knoten sowohl als an den Bäuchen Papierreiterchen aufsetzt; an diesen Punkten werden sie abgeworfen, an jenen bleiben sie sitzen. Während einer Saite die zum Schwingen erforderliche Elastizität durch eine äußere Kraft (die Spannung) mitgeteilt werden muß, besitzen Stäbe aus starrem Material in sich selbst schon hinreichende Elastizität. Am einen Ende ein geklemmt, ist der Stab der in Fig. 9 dargestellten Schwingungsformen fähig, indem er entweder als Ganzes oder 1, 2, 3... Knoten schwingt, sind beide Enden frei, so besitzt er in seiner einfachsten Schwingungsart bereits zwei Knoten (Fig. 10), die etwa um ein Fünftel der Stablänge von den Enden abstehen, und in denen der Stab unterstützt werden muß, um ungehindert schwingen zu können.
Die Schwingungszahl eines Stabes ist seiner Dicke direkt, dem Quadrat der Länge und der Quadratwurzel aus dem spezifischen Gewicht umgekehrt proportional, von seiner Breite dagegen unabhängig. Die Obertöne, die den höhern Schwingungsformen entsprechen, sind nicht mehr zum Grundton harmonisch, wie bei den Saiten, sondern steigen viel rascher in die Höhe. Eine Stimmgabel ist als ein gebogener Stab mit freien Enden zu betrachten, der mit zwei Knoten (Fig. 1 c c) schwingt.
Platten können sich in mannigfaltiger Weise durch Knotenlinien abteilen, wenn man sie am Rande mit dem Violinbogen streicht und gewisse Punkte derselben durch Festklemmen oder Berühren mit dem Finger am Schwingen hindert. Durch ausgestreuten Sand, der sich naturgemäß an den Knotenlinien anhäuft, kann man diese sichtbar machen (Klangfiguren). Glocken sind als schalenförmig gekrümmte Platten anzusehen; beim Tönen zerlegen sie sich ebenfalls in schwingende Abteilungen, die durch ruhende Knotenlinien voneinander getrennt sind. Vgl. Ernst Heinrich und Eduard Wilhelm Weber, Wellenlehre, auf Experimente gegründet (Leipz. 1825); Emy, Über die Bewegung der Wellen (deutsch von Wiesenfeld, Wien 1839).
Buchempfehlung
Schnitzler, Arthur
Der grüne Kakadu. Groteske in einem Akt
In Paris ergötzt sich am 14. Juli 1789 ein adeliges Publikum an einer primitiven Schaupielinszenierung, die ihm suggeriert, »unter dem gefährlichsten Gesindel von Paris zu sitzen«. Als der reale Aufruhr der Revolution die Straßen von Paris erfasst, verschwimmen die Grenzen zwischen Spiel und Wirklichkeit. Für Schnitzler ungewöhnlich montiert der Autor im »grünen Kakadu« die Ebenen von Illusion und Wiklichkeit vor einer historischen Kulisse.
38 Seiten, 3.80 Euro
Im Buch blättern
Ansehen bei Amazon
Buchempfehlung
Geschichten aus dem Biedermeier III. Neun weitere Erzählungen
Biedermeier - das klingt in heutigen Ohren nach langweiligem Spießertum, nach geschmacklosen rosa Teetässchen in Wohnzimmern, die aussehen wie Puppenstuben und in denen es irgendwie nach »Omma« riecht. Zu Recht. Aber nicht nur. Biedermeier ist auch die Zeit einer zarten Literatur der Flucht ins Idyll, des Rückzuges ins private Glück und der Tugenden. Die Menschen im Europa nach Napoleon hatten die Nase voll von großen neuen Ideen, das aufstrebende Bürgertum forderte und entwickelte eine eigene Kunst und Kultur für sich, die unabhängig von feudaler Großmannssucht bestehen sollte. Für den dritten Band hat Michael Holzinger neun weitere Meistererzählungen aus dem Biedermeier zusammengefasst.
- Eduard Mörike Lucie Gelmeroth
- Annette von Droste-Hülshoff Westfälische Schilderungen
- Annette von Droste-Hülshoff Bei uns zulande auf dem Lande
- Berthold Auerbach Brosi und Moni
- Jeremias Gotthelf Die schwarze Spinne
- Friedrich Hebbel Anna
- Friedrich Hebbel Die Kuh
- Jeremias Gotthelf Barthli der Korber
- Berthold Auerbach Barfüßele
444 Seiten, 19.80 Euro
Ansehen bei Amazon
- ZenoServer 4.030.014
- Nutzungsbedingungen
- Datenschutzerklärung
- Impressum